Forecasting
1. Basic Forecasting Tools
1.1 Forecasting Methods and Examples
1.1.1 Examples:
The first example, [Web: Australian Monthly Electricity Production ], displays a clear trend and seasonality. Note
that both the seasonal variability as well as the mean show a
trend.
The data [Web: US Treasury Bill Contracts ] shows a trend, but there is less certainty as to
whether this trend will continue.
The data on [Web: Australian Clay Brick
Production ] contains occasional
large fluctuations which are difficult to explain, and hence predict, without
knowing the underlying causes.
Exercise 1.1: Make Timeplots
of each data set: Australian Monthly Electricity,
US Treasury Bills, Australian Clay Brick.
1.1.2 Quantitative and Qualitative Approach:
Quantitative approach relies on sufficient reliable quantitative
information being available. Qualitative approach is an alternative if expert
knowledge is available.
1.1.3 Explanatory Versus Black-Box Models:
An explanatory model is one that attempts to explain the
relationship between the variable to be forecast and a number of independent
variables. eg
GNP = f(monetary
and tax policies, inflation,
capital spending,
imports, exports) + Error
A time series model is one that attempts to relate the value of
a variable(s) at one time point with values of the variable(s) at previous
time points. eg
GNPt+1 = f(GNPt, GNPt-1,
GNPt-2, ....) + Error
A black-box model is one that simply tries to relate future
values of the variable of interest to previous values, without attempting to
explain its behaviour in terms of other variables.
Thus simple time series models, like the one above, are 'black-box'.
More complex time series models are explanatory in that they try
to relate the value of the variable of interest not simply with its previous
values but also with previous values of other 'explanatory' variables.
1.2 Graphical Summaries
1.2.1 Time plot.
Always make a time plot and look for patterns:
(i) A time series is said to be stationary if
distribution of the fluctuations is not time dependent In particular both the variability
about the mean, as well as the mean must be independent of time.
(ii)
A seasonal/periodic pattern is one with a yearly, monthly or weekly
period.
(iii)
A cyclical pattern is one where there are rises and falls but not of
regular period.
(iv) A trend is a long term increase or decrease in
the variable of interest.
eg [Web:
Australian beer production: Time Plot
]
1.2.2 Seasonal plot.
A seasonal plot is one where the time series is cut into regular
periods and the time plots of each period are overlaid on top of one another.
eg [Web:
Australian beer production: Seasonal
Plot ]
Exercise 1.2: Produce time and seasonal plots
for the Australian beer production data.
1.2.3 Scatterplots.
This plots the relationship between two variables, but does not
necessarily have to have time as one of the variables.
eg [Web:
Price/Mileage relationship for 45 cars ]
Exercise 1.3: Produce a scatterplot
for the Price/Mileage relationship for
45 cars data.
1.3 Numerical Summaries
1.3.1 Statistics.
A statistic is a summary quantity calculated from a data set.
1.3.2 Univariate Statistics.
Commonly used statistics are the mean, median, deviation, mean absolute
deviation (MAD), variance or mean square deviation (MSD); standard deviation (SD).
These are calculated for the data:[Web: 19 Japanese Cars
]
EXCEL contains several of these statistics as Worksheet Functions,
specifically:
AVERAGE, MEDIAN,
VAR, STDEV.
Note: VAR and STDEV now use n – 1 in the divisor. [Also they use an old fashioned version of
the formula, which is not fully robust.]
Exercise 1.4: Reproduce, in a spreadsheet the
calculations made in the example: 19 Japanese Cars.
1.3.3 Bivariate.
The most commonly used statistics for bivariate
data is the covariance, and the correlation coefficient. If we
have n pairs of observations (Xi, Yi) on
two variables X and Y then the formulas are:
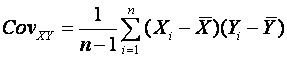
and
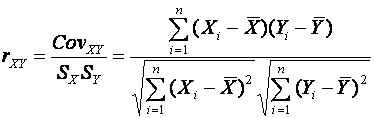
The correlation coefficient is a standardised version of the
covariance and its value is always between -1 and 1. Values close to each limit
indicate a strong linear relation between the two variables.
eg These statistics
are calculated for the data: [Web: 19 Japanese cars (bivariate) ]
EXCEL has the Worksheet Functions: COVAR, CORREL. However COVAR uses n
in the divisor. Why does it not matter whether n or (n-1) is used
for the correlation?
Exercise 1.5: Calculate these statistics for
yourself, and using the Worksheet functions: 19 Japanese Cars.
1.3.4 Autocovariance; Autocorrelation.
The use of covariance and correlation can be extended to a time series
{Yt}. We
can compare Yt
with the previous lagged value Yt-1. The autocovariance, ck, and autocorrelation
at lag k, rk, are
defined as
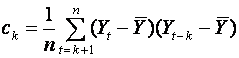
and
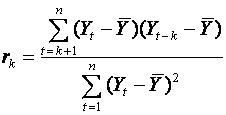
The complete set of autocovariances is called
the autocovariance function, and the
set of autocorrelations, the autocorrelation function (ACF).
Exercise 1.6: Calculate the ACF for the Australian Beer Production data (ACF). [Web: Australian Beer Production ACF. ]
Note that there is a peak at lag 12 and a trough at lag 6. It is not
usual to plot more than n/4 lags, as the number of terms in the
summation being relatively small, means that the estimates of the correlations
for large lags are correspondingly less reliable.
Exercise 1.7: Write a VBA macro to calculate the
autocorrelation function. The macro should have as input the column of n observations,
and should output the autocorrelation function up to lag m = n/4.
1.4 Measures of Accuracy
1.4.1 Forecasting Errors
Let Ft be the forecast value and Yt be the actual observation at
time t. Then the forecast error at time t is defined as
et = Yt
- Ft.
Usually Ft is
calculated from previous values of Yt
right up to and including the immediate preceding value Yt-1.
Thus Ft predicts just one step ahead. In this case Ft
is called the one-step forecast and et
is called the one-step forecast error. Usually we assess error not from
one such et but from n
values. Three measures of error are:
(i) The mean error
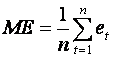
(ii) The mean absolute error
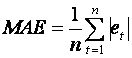
(iii) The mean square error
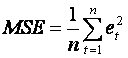 .
.
The mean error is not very useful. It tends to be near zero as positive
and negative errors tend to cancel. It is only of use in detecting systematic
under or over forecasting.
The mean square error is a squared quantity so be careful and do
not directly compare it with the MAE. Its square root is usually similar to the
MAE.
The relative or percentage error is defined as
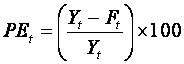
The mean percentage error is
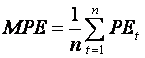
and the mean absolute percentage error is
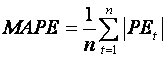
Exercise 1.8: Set up NF1 and NF2 for the Australian Beer Data (NF1, NF2). [Web: Australian Beer Data (NF1,NF2).]
Calculate the ME, MAE, MSE, MPE, MAPE for the Australian beer
series data using NF1 and NF2:
NF1: Ft+1
= Yt
This simply takes the present Y value to be the
forecast for the next period.
The second naive forecast takes into account a seasonal
adjustment. Suppose that the current time point is t = 12m + i where m is the number of complete years
data available. Then, assuming no trend we can take the current monthly
averages for j = 1,2,..., 12 as
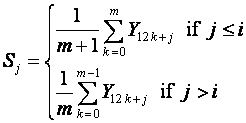
The second naive forecast is then
NF2: Ft+1
= Yt - Si + Si+1
Hint: The summation formula for Sj
is not very convenient to enter directly on a spreadsheet. It is much
easier to use an updating formula instead. It we write St for
the seasonal index corresponding to time t (= 12m + i) ( i.e.
t corresponds to ith month in
the (m+1)th
year), then
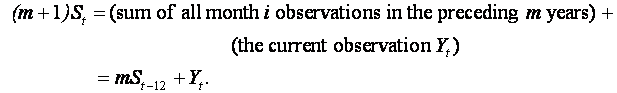
i.e.
![]() .
.
This is the formula used in the spreadsheet.
1.4.2 ACF of Forecast Error.
It is often useful to regard the one-step forecast errors as a time
series in its own right, and to calculate and plot the ACF of this series. This
has been done for the Australian beer production series. [Web: Australian
Beer Data (NF1,NF2).]
Notice that there is pattern in the series and this has been picked up
by the ACF with a high value at lag 12. Do not read too much into the other
autocorrelations as one should expect departures from zero even for the ACF of
a random series.
1.4.3 Prediction Interval.
Assuming that the errors are normally distributed then one can assess
the accuracy of a forecast by using ![]() as an estimate of the
error then an approximate prediction interval for the next observation is
as an estimate of the
error then an approximate prediction interval for the next observation is
![]()
where z is a quantile of the normal distribution. Typical values used
are:
z Probability
1.282 0.80
1.645 0.90
1.960 0.95
2.576 0.99
1.5 Transformations
Sometimes a systematic adjustment of the data will lead to a simpler
analysis. We consider just two forms.
1.5.1 Mathematical Transforms
There are two ideas that are helpful in selecting an appropriate
transform.
First, it is usually easier to analyse a time series is the underlying
mean is constant, or at least varies in a linear way with time. Thus if the behaviour of the actual data has
the form
Yt = at
p + εt
where a and p are
constants and εt is an random
'error', then the transform
Wt
= (Yt)1/p
= (at p + εt)1/p
= bt + δt
,
where b = a1/p,
makes Wt look more
'linear' than Yt . Note that the
transformed 'error', δt,
will depend in a complicated way on εt,
a, p and t. However in many situations the behaviour of δt will remain 'random' looking and
be no more difficult to interpret that the initial error εt .
The above is known as a power transform.
Another useful transform is the logarithmic transform:
Wt = log e (Yt).
This can only be used if Yt
> 0, as the logarithm of a negative quantity is complex valued.
The second idea is that the random errors are most easily handled if
their variability is not time dependent but remains essentially constant. A
good transformation should therefore be variance stabilizing, producing
errors that have a constant variance. For example if
Yt = a(t
+ εt) p
where the εt
have a constant variance, then the power transform
Wt
= (Yt)1/p
= a 1/p(t + εt)
= bt + δt
where b = a1/p
and δt = bεt
will not only linearise the trend, but will also be
variance stabilizing, as δt
will have constant variance.
Finally note that, though we analyse the transformed data, we are
really actually interested in the original sequence. So it is necessary to back
transform results into the original units. Thus, for example in the last
case, we might analyse the Wt and estimate b, by, ![]() say but we would back transform to
estimate a by
say but we would back transform to
estimate a by
![]() .
.
An important but somewhat difficult technical issue is that such
transforms can destroy desirable properties like unbiasedness.
A well known case concerns a random sample X1, X2, ... Xn,
of size n. Here, the sample variance given by the formula
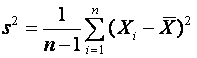
is known to be an unbiased estimator for the
variance. However, s, the obvious estimator for the standard deviation
is not unbiased. When n is large this bias is, however, small.
Exercise 1.9: Plot the Australian
Monthly Electricity data using the square root and the (natural) log
transforms.
[Web: Australian Monthly
Electricity Production ]
1.5.2 Calendar Adjustments.
If data is for calendar months, then account might have to be taken of
the length of a month. The difference between the longest and shortest months
is about (31- 28)/30 = 10%. The adjustment needed is
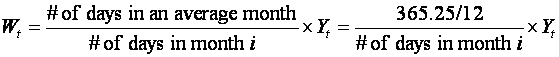
Exercise 1.10:: Make separate time series plots of Yt and Wt for the data on the Monthly Milk production per cow.
[Web: Monthly Milk
]