View this portrait in full.
|
Prof. Dr. Jörg
Fliege, FORS
Please take a look at my
timetable / availability |
Welcome to my
homepage. Don't expect too much from it, since the page is the
result of twenty minutes spare time. You will only find some links I
like and the description of some of my work.
I am interested in mathematical algorithms useful for the design and the optimization of multi-hop ad-hoc wireless networks, especially with respect to routing, power control, decomposition approaches, etc. Most of these algorithms have to work in a distributed fashion in a real-time environment, so their design can be considered as hard. My work is mainly done in conjunction with industrial partners like Alcatel-Lucent, Bell Labs, Qualcomm, etc.
(Photo on the left by Milica Seculic,
photo on the right by smith.
Both used under the creative commons 2.0 license.
Middle photo copyright by Joerg Fliege, Armin Dekorsy, and Joe Hodgskiss.)
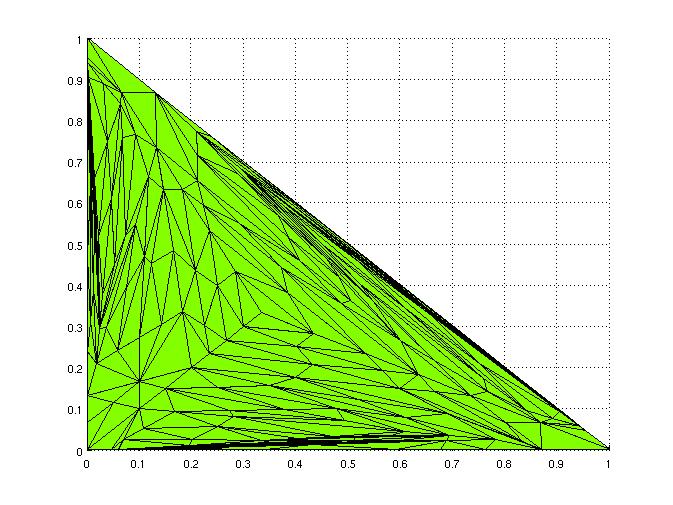
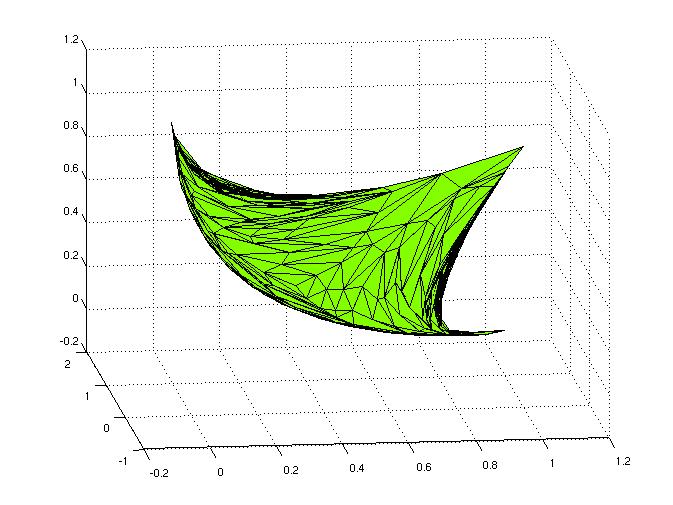
In multicriteria (multiobjective) optimization, several objective functions have to be minimized simultaneously. Usually, no single point will minimize all given objective functions at once, and so the concept of optimality has to be replaced by the concept of Pareto-optimality or efficiency. A point is called Pareto-optimal or efficient, if there does not exist a different point with the same or smaller objective function values, such that there is a decrease in at least one objective function value. Two different efficient points will usually be not only quite different from each other in terms of objective function values, but also incomparable with each other: it will not be the case that one point is better than the other one with respect to all objective functions involved. Instead, the quality of the points will change across different objectives. Therefore, we have to gain as much information as possible about the solution set of a given problem, preferably by constructing a well-defined approximation to it.
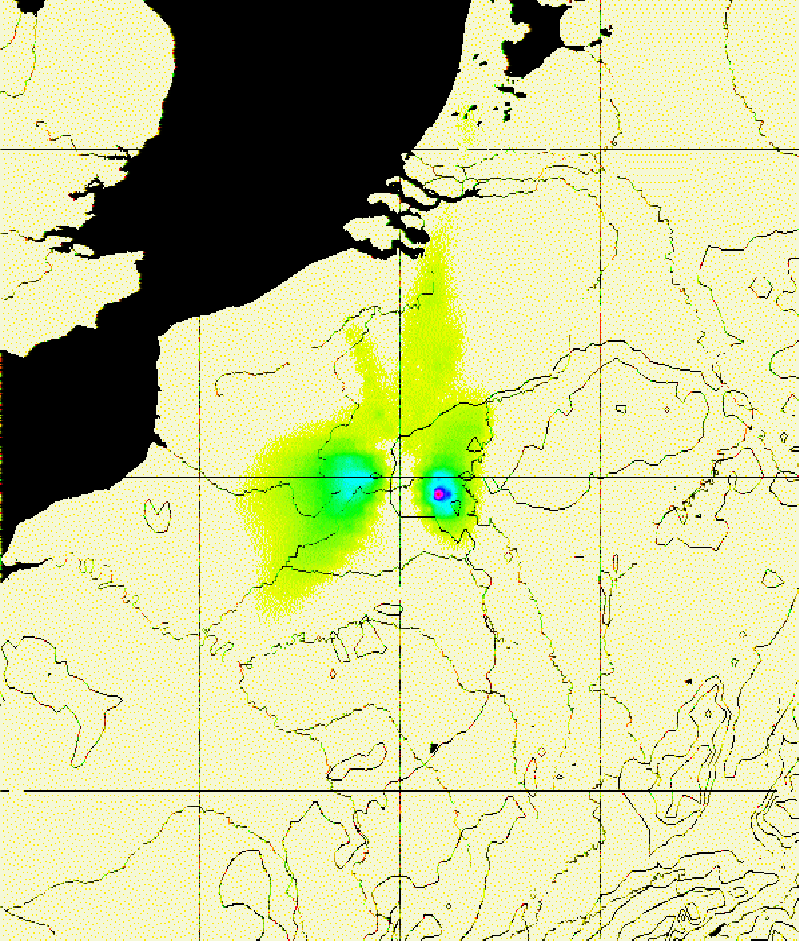
The OLAF software models the effects of a low-toxic air pollutant on inhabitants of arbitrary land-based ecosystems and optimizes the location of the polluting facility.
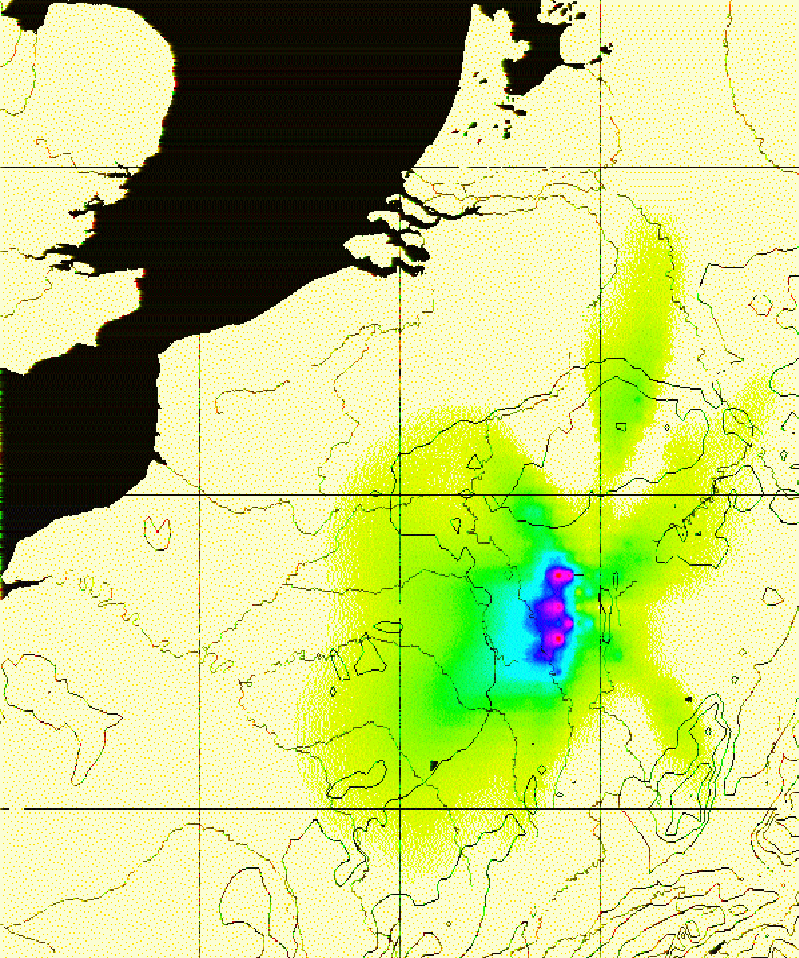
Here you can find more information about one of my current research interests. If you need to integrate functions defined on the two-dimensional sphere $S^2$, this might be what you are searching for.
I was rather angry when I wrote this little piece. Please bear with me.
Search some (rather old) bibliographies (in BibTeX format) online and look at some links to other projects of this kind.
