Forecasting

2. Time Series Decomposition

In this Section we study methods for analysing the structure of a time series. Strictly these techniques are not forecasting methods, but they will be helpful and will be employed in actual forecasting methods.

The basic approach in analysing the underlying structure of a time series is to decompose it as

Y_t = f(S_t, T_t, E_t)

where Y_t is the observed value at time t

S_t is the seasonal component at time t

T_t is the trend-cycle component at time t

E_t is an irregular (random) component at time t

There are several forms that the functional form f can take.

2.1 Additive and Multiplicative models

We have an additive decomposition if

Y_t = S_t + T_t + E_t.

We have a multiplicative decomposition if

Y_t = S_t × T_t × E_t.

This can be converted to an additive model by taking logarithms, as if Y_t = S_t×T_t×E_t , then

logY_t = logS_t + logT_t + logE_t.

It is important to plot the components separately for comparison purposes.

For the additive model it is common to focus on seasonally adjusted data by subtracting the seasonal component from the observations.

Y_t − S_t = T_t + E_t.

The seasonal component is not known and has to be estimated so the seasonally adjusted data will take the form Y_t − . Here and in what follows we use a circumflex to denote an estimate.

An important point to note is that in analysing a time series it is usually better to estimate the trend-cycle first, then estimate the seasonality.

But before even this, it is best to reduce the effect of the irregular component by smoothing the data. So this is usually done first.

2.2 Smoothing

One can in principle regard smoothing as being carried out to remove the effect of the irregularity alone. This will leave both the time-cycle and seasonal components, which then have to be distinguished one from the other.

However, if a seasonal component is expected, then it is more usual to apply the smoothing in such a way that the seasonal component as well as the irregular component are both removed. This then leaves just the trend-cycle, which is therefore identified!

Using this latter approach we can then immediately remove the trend cycle by subtraction

D_t = Y_t − T_t = S_t +E_t

and then identify the seasonality from this de-trended time series. It should be noted that smoothing only produces an estimate, , of the trend-cycle

Thus the de-trended time series should strictly be written as

We will see shortly that identification of seasonality from a de-trended time series (or from a time series in which there was no trend-cycle in the first place), is easy.

2.2.1 Moving Average

A simple way to carry out smoothing is to use a moving average. The basic idea is that values of observations which are close together in time will have trend-cycle components that are similar in value. Ignoring the seasonal component for the moment, the value of the trend-cycle component at some particular time point can then be obtained by taking an average of a set of observations about this time point. Because the values that are averaged depend on the time point, this is called a moving average.

There are many different forms that a moving average can take. Many have been constructed using ad-hoc arguments and reasoning. All boil down to being special cases of what is called a k-point weighted moving average.

.

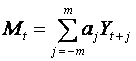where m = (k-1)/2 is called the half-width, and the a_j are called the weights.

Note that in this definition k must be an odd number. The simplest versions are the where all the weights are the same. This is then called a simple moving average of order k.

eg if k = 3, then M_t = (Y_t-1 + Y_t + Y_t+1)/3.

If the weights are symmetrically balanced about the centre value (ie about j = 0 in the sum), then this is called a centred moving average.

Simple moving averages involving an even number of terms can be used, but are then not centred about an integer t. This can be redressed by averaging a second time only averaging the moving averages themselves. Thus, for example, if

M_2.5 = (Y₁ + Y₂ + Y₃ + Y₄)/4 and M_3.5 = (Y₂ + Y₃ + Y₄+Y₅ )/4

are two consecutive 4-point moving averages, then we can centre them by taking their average

(M_2.5 + M_3.5)/2 = (Y₁ + 2Y₂ + 2Y₃ + 2Y₄+Y₅ )/8.

This example is called a 2×4 MA. It is simply a 5-point weighted moving average, with end weights each 1/8, and with the other three weights = ¼.

If applied to quarterly data, this 2×4 MA, would give equal weight to all four quarters, as the 1st and last values would apply to the same quarter (but in different years). Thus this smoother would smooth out quarterly seasonally variation.

Similarly a 2×12 MA would smooth out seasonal variation in monthly data.

Exercise 2.1: What are the weights of a 2×12 MA smoother?

Exercise 2.2: Fit 7MA and 2x12MA moving averages to the Housing Sales Data [Web: Housing Sales Data]

There are a number of weighting schemes proposed. All tend to have weight values that tail off towards the two ends of the summation. Also they are usually symmetric with a_j = a_-j. There is a problem applying a moving average at the two ends of a time series when we run out of observations to calculate the complete summation. When fewer than k observations are available the weights are usually rescaled so that they sum to unity.

An effect of a moving average is that it will underestimate trends at the ends of a time series. This means that the methods discussed so far are generally unsatisfactory for forecasting purposes when a trend is present.

2.3 Decomposition

In this section we consider what might be called classical decomposition. These are methods developed in the 1920's which form the basis of typical existing decomposition methods. The consider the additive and the multiplicative cases and where the seasonal period is 12.

2.3.1 Additive Decomposition

This is for the case where Y = T+S+E. The classical decomposition takes four steps.

Step 1: Compute the centred 12 MA. Denote this series by M_t. This series estimates the trend-cycle.

Step 2: De-trend the original series by subtraction:

D_t = Y_t − M_t = S_t +E_t

Step 3: Calculate a seasonal index for each month by taking the average of all the values each month, j:

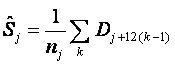
In this formula, it is assumed that there are n_j values available for month j, so that the summation is over these n_j values.

Step 4: The estimated irregularity is obtained by subtraction of the seasonal component from the de-trended series:

.

Here denotes the seasonal index for the month corresponding to observation Y_t.

2.3.2 Multiplicative Decomposition

For the multiplicative model Y = T×S×E the method is called the ratio of actual to moving averages. There are again four steps.

Step 1: Compute the centred 12 MA. Denote this series by M_t. This step is exactly the same as in the additive model case.

Step 2: Calculate R_t, the ratio of actual to moving averages:

.

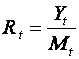Step 3: Calculate a seasonal index for each month by taking the average of all the values each month, j:

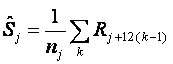
This step is exactly the same as in the additive case except that D is replaced by R.

Step 4: Calculate

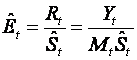
Exercise 2.3: Analyse the House Sales Data using the additive model. Plot the trend-cycle, seasonal and irregular estimates.

Note: This exercise gives you practice in using the pivot table to calculate the seasonal adjustments.

[Web: House Sales Data ]

Exercise 2.4: Analyse the International Airline Data using the multiplicative model. Plot the trend-cycle, seasonal and irregular estimates. [Web: International Airline Data ]