An efficient optimization algorithm needs necessarily local information
of higher order about the objective function. While there does not
seem to be a simple way to compute 
and
, the gradient with respect to the locational
decision variables 
(which are arguably the most important ones) can
be approximated in the following way. Under suitable differentiability
assumptions and integrability of 
, we have that
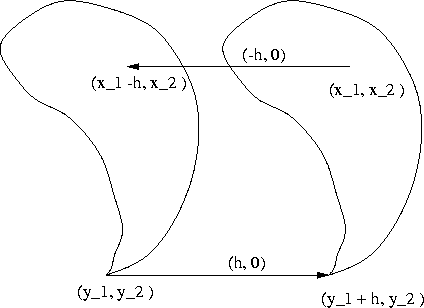
Figure 5.1: Translating the origin
of the pollutant source results in a translation of the
pollutant cloud and of the effect.
Taking a look at Figure 5.1, it is reasonable to
make the assumption
for 
. As a consequence, for
we get
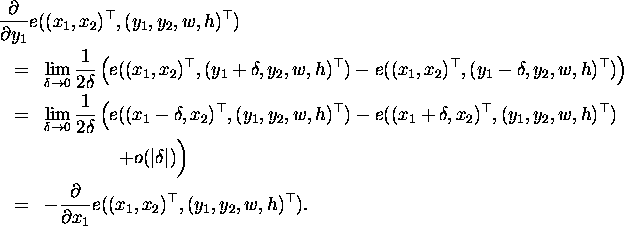
This is the approach chosen in OLAF. The differentials
are approximated by finite differences of third
order, where the discretization size is exactly the grid size of the
computational grid in 
-direction. In this way, the approximations
to on the grid discretizing G are used to calculate
the differential of , and no further simulation run
of the dispersion model or the cytodynamic model is necessary.
Under analogous assumptions, the same reasoning holds for
. Additional objective function evaluations due to
time-intensive numerical differentiation routines can therefore
be avoided. Computational tests showed that the use of this scheme results
in a large decrease in computation time, although the total number of
iterations increases slightly when compared to an implementation where
central differences have been used to approximate the gradient of the
objective function. This might be attributed to the fact that in practical
applications the accuracy of the approximation scheme above is lower than
central differences. Consequently, descent algorithms which employ
local information of higher order need more iterations, but less
total computation time.
We may go even one step further. Using (5.3) and partial
integration, we see that
holds whenever G has a smooth boundary and the function
has compact support. Here, 
is the
outer normal of G at a boundary point 
.
By choosing G large enough (or choosing a population distribution p
with compact support small enough), we can make sure that the boundary
integral gets arbitrary small, and we can approximate the
differential of f with respect to 
by
Since 
is independent of 
, it can
be computed or approximated in whatever way necessary before any optimization
takes place. Approximating 
then involves
only the evaluation of the integral in (5.4), which can be done in
the same way as the evaluation of f at .
Unfortunately, none of these schemes works for the derivatives with respect to stack height and stack diameter. As a consequence, numerical differentiation with central differences is used to approximate the derivative of f with respect to h and w.
A different possibility would be to use automatic differentiation to compute derivatives of f with respect to h and w. Preliminary numerical experience [25, Chapter 1,] suggests that this approach is computationally very expensive for parametrized air dispersion models. No effort has been made to use automatic differentiation within OLAF.