Note that all entries in the system matrix of (3.3) except those on
the diagonal are nonnegative, while the diagonal entries are nonpositive.
Moreover, the inhomogeneous part is nonnegative (or, more precisely, strictly
positive for compartment ![]() ) if and only if the air compartment
contains a positive pollutant mass and there is an exchange between the air
compartment and compartment k. Consider for the moment the case that the
inhomogeneous part is zero, i. e.
) if and only if the air compartment
contains a positive pollutant mass and there is an exchange between the air
compartment and compartment k. Consider for the moment the case that the
inhomogeneous part is zero, i. e. ![]() or
or
![]() , and
that no backflow to the air compartment takes place, i. e.
, and
that no backflow to the air compartment takes place, i. e.
![]() . As a consequence,
all column sums of the matrix A (t) are zero for all t, and any consistent
multistep or Runge-Kutta method for solving (3.3) will lead to mass
consistency, regardless what step size is used and no matter if the method is
explicit or implicit.
. As a consequence,
all column sums of the matrix A (t) are zero for all t, and any consistent
multistep or Runge-Kutta method for solving (3.3) will lead to mass
consistency, regardless what step size is used and no matter if the method is
explicit or implicit.
Due to (3.1) and the theorem of Gershgorin, the eigenvalues
of A (t) have only nonpositive real parts (for all ![]() ), and the only
possible eigenvalue with real part equal to zero is 0. This makes the system
stiff, while a lower bound for the real part of the eigenvalues at time t is
), and the only
possible eigenvalue with real part equal to zero is 0. This makes the system
stiff, while a lower bound for the real part of the eigenvalues at time t is
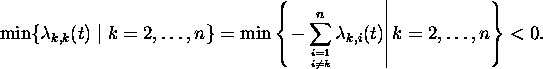
At first glance an implicit numerical solver should be used to
solve (3.3). But implicit methods require the solution of
a linear system in n-1 variables per time step. In contrast to this, an
explicit solver just needs one matrix-vector multiplication to compute
the next approximation. Moreover, the accuracy demand in the application
discussed here is rather moderate, since the inhomogeneous part
of (3.3) cannot be calculated with high accuracy. As a consequence,
we use Euler's method in the present implementation of the compartment model
within OLAF. Nonnegativity of the iterates is achieved by the following
step size control. In the homogeneous case, we have
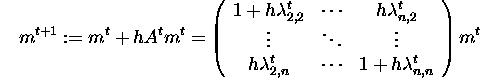
as the iteration procedure. Here, the superscripts denote the time steps
for the approximations ![]() that we compute with
step length h > 0. Given a (componentwise) nonnegative vector
that we compute with
step length h > 0. Given a (componentwise) nonnegative vector ![]() , the
nonnegativity of
, the
nonnegativity of ![]() can be assured if
can be assured if ![]() for
for ![]() . The step size chosen by OLAF is then
. The step size chosen by OLAF is then
![]()
the largest one possible under this constraint. Note that larger step sizes
can also be allowed, e. g. if
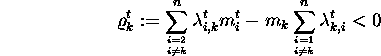
for a ![]() ,
, ![]() , then use a step size h with
, then use a step size h with
![]()
This rule depends then on the values of ![]() . Even larger steps can be made
if the inhomogeneous term is used in the above estimate:
. Even larger steps can be made
if the inhomogeneous term is used in the above estimate:
![]()
for all ![]() with
with ![]() .
.
With the implicit Euler method,
![]()
i. e.
![]()
one may use arbitrary step sizes h > 0 without violating the
nonnegativity of ![]() . This can be seen in the following way.
The unique solution
. This can be seen in the following way.
The unique solution ![]() of the homogeneous version
of (3.3),
of the homogeneous version
of (3.3),
![]()
is nonnegative. Now write A(t) = N(t) - D(t) with the positive diagonal
matrix ![]() and
define the operator
and
define the operator
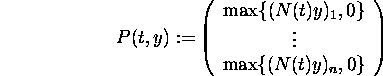
for arbitrary vectors ![]() and
and ![]() . Note that
. Note that
![]() for all y and all
for all y and all ![]() . With this, the system of
differential equations
. With this, the system of
differential equations
![]()
has a unique solution ![]() . But then
. But then ![]() , and
consequentially
, and
consequentially
![]() for all
for all ![]() . Therefore, employing the implicit Euler method
on (3.10) leads to the same approximations
. Therefore, employing the implicit Euler method
on (3.10) leads to the same approximations ![]() as if the method has been used to solve (3.9).
But then
as if the method has been used to solve (3.9).
But then
![]()
and when the right hand side is nonnegative (by induction), ![]() will also be nonnegative. Note that this reasoning works only if the
system of linear equations (3.8) is solved exactly,
i. e. with a direct method and not an iterative one. Therefore,
a nonnegativity enforcing version of Euler's implicit method needs
will also be nonnegative. Note that this reasoning works only if the
system of linear equations (3.8) is solved exactly,
i. e. with a direct method and not an iterative one. Therefore,
a nonnegativity enforcing version of Euler's implicit method needs
![]() floating point operations per time step, as compared
to the
floating point operations per time step, as compared
to the ![]() floating point operations for the explicit version.
More precise estimates depend on the sparsity structure of the system
matrix A.
floating point operations for the explicit version.
More precise estimates depend on the sparsity structure of the system
matrix A.
Note, however, that computing an approximative solution of this system
of ordinary differential equations is necessary for each point of the
computational grid of the air dispersion code, and that any step size rule
depending on ![]() decouples the time grid of the different systems to be
solved. This poses a problem when the actual objective function has to be
evaluated, because each mass in each compartment is then also equipped with
a time interval representing the length of stay of the mass inside the
compartment. Due to this, further tests with step size rules
like (3.6) or (3.7) have been postponed.
decouples the time grid of the different systems to be
solved. This poses a problem when the actual objective function has to be
evaluated, because each mass in each compartment is then also equipped with
a time interval representing the length of stay of the mass inside the
compartment. Due to this, further tests with step size rules
like (3.6) or (3.7) have been postponed.
While atmospheric dispersion models usually use a rather large time scale, chemokinetic models do not. Typical time steps in atmospheric dispersion are one hour or several hours, while the scale needed in the chemokinetic model is, according to what is said above, only minutes. As a consequence, the concentration of the pollutant in the air as used in the ecosystem dispersion and the chemokinetic model is approximated by a piecewise constant function. While it is possible to compute out of this data a smooth approximation, it is not clear how mass balance can be achieved. On the other hand, nonsmooth right-hand sides in (3.3) pose serious numerical problems to the corresponding solver. Due to this, Euler's method is used only from one time step of the atmospheric dispersion model to the next. The last step size used in Euler's method is computed in such a way that the step taken coincides with the end point of the interval in which the current constant approximation of pollutant concentration in the air holds. The next step of Euler's method uses the new pollutant concentration from the next time step of the atmospheric dispersion model.