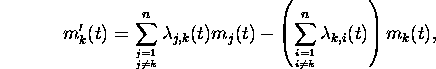
where
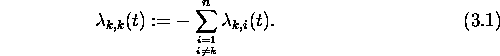
When using the vector notation
hold, where the starting condition m(0) depends on the spatial location, i. e. the grid point of the computational grid used. Note that the function
Both the ecosystem dispersion model and the chemokinetic model are described in this chapter, since the modeling paradigm used for the two submodels is the same.
The ecosystem dispersion model takes as input the time- and space-dependent air concentration of the pollutant at the predefined grid points and follows the fate of the pollutant across the different trophic levels of the ecosystems considered. Each grid point of the air dispersion model represents one local food web, through which the trace of the pollutant is followed.
Note that population dynamics are not accounted for, since there does not seem to be a general mechanism for population dynamics, valid for all kinds of interacting populations [10, 28].
The chemokinetic model takes as input the time- and space-dependend exposure of an individual to the pollutant under consideration and computes the uptake and the distribution of the chemical in the different body tissues and organs. Several different types of individuals can be simulated by specifying the corresponding parameters. The metabolism of the pollutant under consideration is modeled by Michaelis-Menten kinetics.
Both codes simulating the processes described above are based
on a compartment model of the system to be
simulated [19, ] (also called continuously
stirred tank reactor (CSTR) model). These systems are of the following
type, and one of these systems is set up for each grid point of
the computational grid of the atmospheric dispersion model. The modeler divides
the total system under consideration (i. e. the ecosphere and the geosphere)
into ![]() different compartments. The total mass of pollutant
over time in a compartment k,
different compartments. The total mass of pollutant
over time in a compartment k, ![]() , is then given by a function
, is then given by a function
![]() , which has to be computed. Again,
note that we have
, which has to be computed. Again,
note that we have ![]() where
where ![]() is a variable
denoting the point in space where the compartment system resides. In what
follows, we skip this dependency for ease of notation. In the
compartment model implemented in OLAF, compartment no. 1 is always
the "air compartment", and the total mass in it is represented by the pollutant
concentration calculated by the MESOPUFF II model (see
Section 2.2). As a consequence, the function
is a variable
denoting the point in space where the compartment system resides. In what
follows, we skip this dependency for ease of notation. In the
compartment model implemented in OLAF, compartment no. 1 is always
the "air compartment", and the total mass in it is represented by the pollutant
concentration calculated by the MESOPUFF II model (see
Section 2.2). As a consequence, the function ![]() can be considered
as an external variable which does not need to be calculated here any more.
By the first law of thermodynamics, the change of mass in compartment no. k
(
can be considered
as an external variable which does not need to be calculated here any more.
By the first law of thermodynamics, the change of mass in compartment no. k
(![]() ),
), ![]() , is the difference between the
inflow and the outflow to other compartments. The inflow from compartment
no.
, is the difference between the
inflow and the outflow to other compartments. The inflow from compartment
no. ![]() to compartment no. k is proportional to the mass inside
compartment j, while the outflow out of compartment k to compartment
no. i is proportional to the mass in compartment k. As a consequence,
the following ordinary differential equation holds for
to compartment no. k is proportional to the mass inside
compartment j, while the outflow out of compartment k to compartment
no. i is proportional to the mass in compartment k. As a consequence,
the following ordinary differential equation holds for ![]() :
:
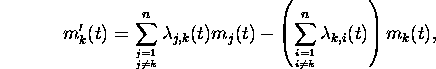
where ![]() is the time-dependent proportionality
constant for the flow from compartment j to compartment k, and
is the time-dependent proportionality
constant for the flow from compartment j to compartment k, and
![]() is the time-dependent proportionality constant for the
flow from compartment k to compartment i (
is the time-dependent proportionality constant for the
flow from compartment k to compartment i (![]() ). These
parameters are dimensionless. The differentiation symbol denotes
differentiation with respect to t. Again, we have suppressed
in the notation used here any dependency on the spatial grid point considered.
In what follows, we assume without loss of generality
). These
parameters are dimensionless. The differentiation symbol denotes
differentiation with respect to t. Again, we have suppressed
in the notation used here any dependency on the spatial grid point considered.
In what follows, we assume without loss of generality
![]() for
for ![]() and
all
and
all ![]() , i. e. at any time there is at least one inflow into each
non-air compartment considered. Define now the matrix
, i. e. at any time there is at least one inflow into each
non-air compartment considered. Define now the matrix
![]() by using, as usual,
by using, as usual,
![]() as the entry in row k and column i and define the
diagonal elements by
as the entry in row k and column i and define the
diagonal elements by
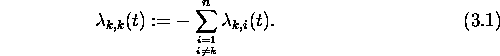
When using the vector notation ![]() ,
we see that the equations
,
we see that the equations
![]()
hold, where the starting condition m(0) depends on the spatial location,
i. e. the grid point of the computational grid used. Note that the
function ![]() is given and does not have to be computed.
is given and does not have to be computed.
In the current version of the OLAF system, a back flow from an
arbitrary compartment to the air compartment is not handled, since it has to
be expected that the quantities involved flowing back are too small to be
tracked numerically once they are added to the large amount of mass
in the air compartment. As a consequence, it is possible to use values
![]() for some
for some ![]() to model a release of
pollutant from a compartment to the air. But, while the mass-balance of the
compartments
to model a release of
pollutant from a compartment to the air. But, while the mass-balance of the
compartments ![]() is correctly computed (i. e. a certain mass
is deducted), the corresponding mass-balance of the air compartment is
not taken into account. Moreover, instead of the mass of the air
compartment, the concentration in it is computed by MESOPUFF.
This means that instead of dimensionless scalars
is correctly computed (i. e. a certain mass
is deducted), the corresponding mass-balance of the air compartment is
not taken into account. Moreover, instead of the mass of the air
compartment, the concentration in it is computed by MESOPUFF.
This means that instead of dimensionless scalars ![]() (
(![]() ) values
) values ![]() with dimension
with dimension
![]() have to be used. Now let c(t) be the concentration of pollutant
in the air at the time
have to be used. Now let c(t) be the concentration of pollutant
in the air at the time ![]() . (Again, we suppress the dependence on the
spatial scale.) We then have to solve the system
. (Again, we suppress the dependence on the
spatial scale.) We then have to solve the system
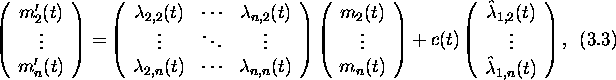
which is a linear inhomogeneous system of ordinary differential equations
of dimension n-1.