(see, e. g., [14, 30]; arguments in the formula above have been omitted). Here,
The air dispersion model takes as input the data computed by the meteorological preprocessor, the locational characteristics of the polluting facility, and the physical and chemical characteristics of the pollutant, and computes out of this given data the concentration of the pollutant in the air at ground level within the time window considered.
Let ![]() be the domain of interest. For a
point
be the domain of interest. For a
point ![]() and a time t > 0, we are interested in the
pollutant concentration c(x, t) at the point x at time t. We assume
that the pollutant concentration at time t = 0 is known everywhere.
As additional data, let a wind field
and a time t > 0, we are interested in the
pollutant concentration c(x, t) at the point x at time t. We assume
that the pollutant concentration at time t = 0 is known everywhere.
As additional data, let a wind field
![]() , a source
term
, a source
term ![]() and a
depletion term
and a
depletion term ![]() be given. The source term represents an input of pollutant into the
atmosphere by way of, e. g., a polluting facility, while the depletion
term represents deposition of the pollutant on the ground. The
advection-diffusion equation governing the pollutant concentration in
be given. The source term represents an input of pollutant into the
atmosphere by way of, e. g., a polluting facility, while the depletion
term represents deposition of the pollutant on the ground. The
advection-diffusion equation governing the pollutant concentration in ![]() is then given by
is then given by
![]()
(see, e. g., [14, 30]; arguments in the formula above
have been omitted).
Here, ![]() is the diffusion matrix. Note that the formulation
above uses Cartesian coordinates, which means that we assume the
earth is flat. If several different pollutants are considered, the
quantity c(x, t) is a vector in the
is the diffusion matrix. Note that the formulation
above uses Cartesian coordinates, which means that we assume the
earth is flat. If several different pollutants are considered, the
quantity c(x, t) is a vector in the ![]() , where n is
the number of pollutants. The formulation above then still applies,
and equation (2.1) has to be interpreted as an
equation in
, where n is
the number of pollutants. The formulation above then still applies,
and equation (2.1) has to be interpreted as an
equation in ![]() . However, chemical reactions between the different
pollutants have then to be taken into account also, and an additional
reaction term
. However, chemical reactions between the different
pollutants have then to be taken into account also, and an additional
reaction term ![]() , which is usually modeled
as a quadratic function in c, has to be added to the formulation above.
, which is usually modeled
as a quadratic function in c, has to be added to the formulation above.
The amount of literature concerning solution methods to
solve (2.1) is monumental, see, e. g. the review
article [32], which lists more than 100 different algorithms.
We will make use here of a particular scheme which exploits the fact
that (2.1) has an analytic solution in the special case
![]() for all (x, t),
for all (x, t), ![]() , I a
Dirac functional of the form I(z, 0) = m > 0 and I(x, t) = 0 for all
, I a
Dirac functional of the form I(z, 0) = m > 0 and I(x, t) = 0 for all
![]() , and c(x, 0) = 0 for all
, and c(x, 0) = 0 for all ![]() . This means that
the only polluting source in
. This means that
the only polluting source in ![]() is at the point
is at the point ![]() , and it
injects once an amount m of pollutant into the atmosphere. Assuming,
additionally,
, and it
injects once an amount m of pollutant into the atmosphere. Assuming,
additionally, ![]() , we get the solution
, we get the solution
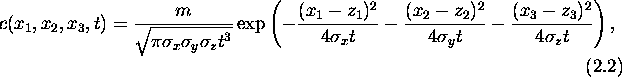
which can be interpreted as a Gaussian "puff" in three-dimensional space
around the origin. Here, ![]() ,
, ![]() , and
, and ![]() are the
dispersion parameters. Other types of solutions exist under
similar conditions [39, Chapter 6,], [29, 37].
are the
dispersion parameters. Other types of solutions exist under
similar conditions [39, Chapter 6,], [29, 37].
The basic strategy is now to discretize the given nonhomogeneous wind field
and approximate it by a piecewise constant function. In each region
of continuity of the approximation, the concentration function c can then
be discretized according to (2.2) into a finite number of puffs,
which are emitted at the pollutant point at discrete time steps. These
puffs are then advected through the (original) wind field according to
the trajectory that the movement of the puff center defines in the field.
The trajectory path x(t) (![]() ,
, ![]() the emitter time) of
a puff center is computed by solving the nonlinear ordinary
differential equation
the emitter time) of
a puff center is computed by solving the nonlinear ordinary
differential equation
![]()
Since the wind field is computed by the preprocessor at the predefined grid
points only, it has to be interpolated, which is usually done bilinearly in
time and space. The dispersion parameters, which are time- and space-dependent,
are updated for each puff separately. Note that this dispersion model is
mass-conservative, a feature of high importance in air pollution
modeling [30, 41].
The air dispersion code used in OLAF is a modified version of the MESOPUFF II puff superposition code [33, 39, 6]. The MESOPUFF II code is able to simulate the dispersion of several different pollutants on a regional scale, i. e. on a scale of ca. 1000km in west-east direction and ca. 600km in north-south direction. This makes the package suitable for medium to long-range transportation simulation. The ordinary differential equation (2.3) which has to be solved to advect the puffs through the wind field is solved with a Runge-Kutta-formula of order 2 given by the Butcher scheme [11]
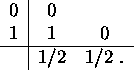
The dispersion parameters are recalculated after each time step
according to empirical update formulae. If the puff center has traveled
less than 100km, they take the familiar form ![]() (cmp. [38, 42]), where
a, b are coefficients calculated according to the stability of the
atmosphere at the present point and d is the total distance the puff
center has traveled. For larger distances, other update formulae are
used [13].
(cmp. [38, 42]), where
a, b are coefficients calculated according to the stability of the
atmosphere at the present point and d is the total distance the puff
center has traveled. For larger distances, other update formulae are
used [13].
Simple atmospheric chemistry as well as wet and dry deposition processes are handled, too. Deposition processes are handled in a mass-conservative way, again. All the deposition takes place on the predefined Cartesian grid. Moreover, several pollutant sources including polluting areas can be present in the computational domain. In this way, a background pollution of the atmosphere can be modeled. After the dispersion model has been run, the concentration data computed can be found in a binary file. If fluxes to the ground are calculated, too, the corresponding gridded data is written to additional binary files.
As it is the case for the preprocessor, the air dispersion code can be replaced by an arbitrary code capable of computing approximations to the desired values as long as the format of the input and the output stays the same. Otherwise, some coding effort to provide the corresponding translation routines is needed.
More details with respect to the dispersion model can be found in the user's manual [39] and in an application protocol [6].