Computer Analysis of Data and Models

 

Part III

 

7.  Empirical Distribution Functions

 

Consider first a single random sample of observations , for i  = 1, 2, ..., n. The empirical distribution function (EDF) is defined as:

 

.                                                                     (27)

 

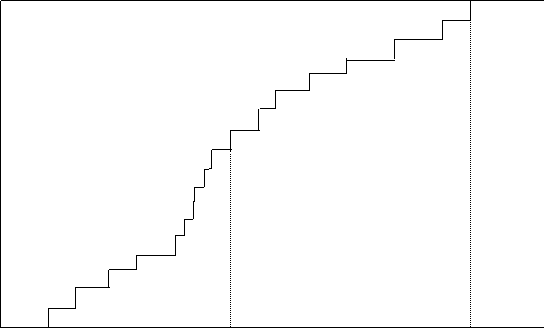
The EDF is illustrated in Figure 6. It is usually simplest to think of the observations as being ordered:

 

Y(1) < Y(2) < … < Y(n) .                                                                       (28)

 

Figure 6: EDF of the Yi ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Y(1)
 

Y(j)
 

Y(n)
 
 

 

 

 

 


These are what are depicted in Figure 6. Note that the subscripts are placed in brackets to indicate that this is an ordered sample.

 

The key point is that the EDF estimates the (unknown) cumulative distribution function (CDF) of Y.  We shall make repeated use of the following:

 

Fundamental Theorem of Sampling: As the size of a random sample tends to infinity then the EDF constructed from the sample will tend, with probability one, to the underlying cumulative distribution function (CDF) of the distribution from which the sample is drawn.

 

(This result when stated in full mathematical rigour, is known as the Glivenko-Cantelli Lemma, and it underpins all of statistical methodology. It guarantees that study of increasingly large samples is ultimately equivalent to studying the underlying population.)

In the previous section we studied the CDF of the Yi ’s of a random sample by fitting a parametric distribution and then studying the fitted parameters and the fitted parametric CDF. Using the EDF, we can do one of two things:

 

(i)      We can study the properties of the Yi  directly using the EDF, without bothering to fit a parametric model at all.

 

(ii) We can use the EDF to study properties of the fitted parameters and fitted parametric distribution.

 

We shall discuss both approaches. We shall focus first on (ii) as we wish to utilise bootstrapping to give us an alternative way of studying the properties of MLE’s, to that provided by asymptotic normality theory which was discussed in Section 6.

 

We postpone discussion of (i) until later. We simply note at this juncture that the attraction of using the EDF directly, rather than a fitted parametric CDF, is that we make no assumption about the underlying distributional properties of Y. Thus Y can be either a continuous or a discrete random variable. Nor is it assumed to come from any particular family of distributions like the normal or Weibull. This flexibility is particularly important when studying or comparing the output from complex simulations where it is possible that the distribution of the output may be unusual. For example it may well be skew, or possibly even multimodal.

 

8.  Basic Bootstrap Method

 

The basic process of constructing a given statistic of interest is illustrated in Figure 7. This depicts the steps of drawing a sample Y = (Y1, Y1, ..., Yn) of size n from a distribution F0(y), and then the calculating the statistic of interest T from Y. The problem is then to find the distribution of T.

 

Bootstrapping is a very general method for numerically estimating the distribution of a statistic. It is a resampling method that operates by sampling from the data used to calculate the original statistic.

 

Bootstrapping is based on the following idea. Suppose we could repeat the basic process, as depicted in Figure 7, a large number of times, B say. This would give a large sample {T1, T2,..., TB} of test statistics, and, by the Fundamental Theorem of Section 3, the EDF of the Ti will tend to the CDF of T as B tends to infinity. Thus, not simply does the EDF estimate the CDF, it can be made accurate to arbitrary accuracy at least in principle, simply by making B sufficiently large.

 

 

 

 

 

Figure 7: Basic Sampling Process


 

 

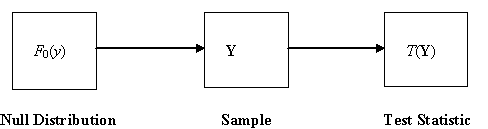
Unfortunately to apply this result requires repeating the basic process many times. In the present context this means having to repeat the simulation trials many times - something that is certainly too expensive and impractical to do.

 

The bootstrap method is based on the idea of replacing F0(y) by the best estimate we have for it. The best available estimate is the EDF constructed from the sample Y.

 

Thus we mimic the basic process depicted in Figure 7 but instead of sampling from F0(y) we sample from the EDF of Y. This is exactly the same as sampling with replacement from Y. We carry out this process B times to get B bootstrap samples Y1*, Y2*, ..., YB*. (We have adopted the standard convention of adding an asterisk to indicate that a sample is a bootstrap sample.) From each of these bootstrap samples we calculate a corresponding bootstrap statistic value Ti* = T(Yi*), i = 1, 2, ..., B. The process is depicted in Figure 8.

 

 


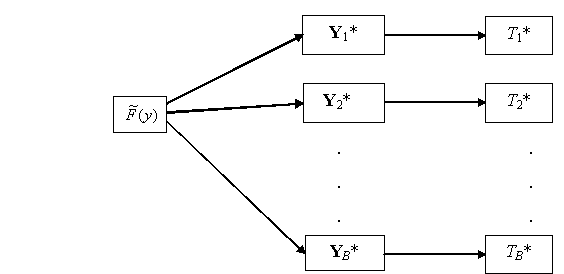
Figure 8: Bootstrap Process

 

 

Example 12: The following is a random sample of 15 observations from an unknown distribution for which the sample median has been obtained. Obtain 90% confidence limits for the unknown true sample median, assuming that the sample is normally distributed. (You will probably have to consult the literature to find the answer to this.)

 

Now calculate 90% confidence limits using bootstrapping.  Bootstrap Median       □

 

 

The EDF of the bootstrap sample, which without loss of generality we can assume to be reordered, so that T(1)* < T(2)* < ... < T(B)*, now estimates the distribution of T. This is depicted in Figure 9. Figure 9 also includes the original statistic value, T0. Its p-value, as estimated from the EDF, can be read off as

 

.                                                           (29)

 

If the p-value is small then this is an indication that T0 is in some sense unusual. We shall see how this idea can be developed into a full methodology for making different kinds of comparisons.

 

 


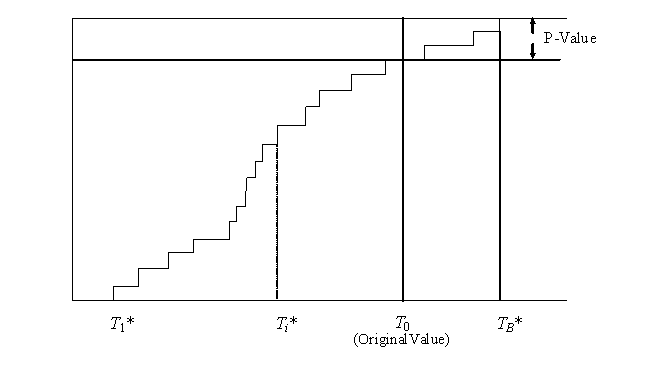
Figure 9: Empirical Distribution Function of the T(i)

In practice typical values of B used for bootstrapping are 500 or 1000, and such a value is generally large enough. With current computing power resampling 1000 values is, to all intents and purposes, instantaneous.

 

Chernick (1999) shows how generally applicable is the bootstrap listing some 83 pages of carefully selected references! A good handbook for bootstrap methods is Davison and Hinkley (1997).

 

We stress that they all hinge on the basic idea set out in this section: namely that replication of the original process depicted in Figure 7 would allow the distribution of T to be obtained to arbitrary accuracy but that this is rarely possible; however the bootstrap version of this process as depicted in Figure 8 is possible and is easy to do. The bootstrap samples are trivially easy to obtain using the algorithm given below in Section 9. There is no problem in calculating the bootstrap statistics Ti* from the bootstrap samples Yi*, as the procedure for doing this must already have been available to calculate T from Y.

 

All the remaining examples discussed in the course are essentially an application of the bootstrapping process of Figure 8 (and its parametric variant, which we will be describing in Section 11), with whatever procedure is necessary inserted to calculate T from Y.

 

9.  Evaluating the Distribution of MLEs by Bootstrapping

 

Let us apply the bootstrapping idea to the evaluation of the distribution of MLE’s. All that is required is to simply treat the MLE,  as being the statistic T of interest!

 

All we need to do is to follow the scheme depicted in Figure 8. We generate bootstrap samples by resampling with replacement from the original sample. Then we use the code to produce the bootstrap T from this sample. The pseudocode for the entire bootstrap process is as follows:

 

          //  y = (y(1), y(2), ..., y(n)) is the original sample.

          //  T=T(y) is the calculation that produced T from y.

          For k = 1 to B

          {

              For i = 1 to n

              {

                   j = 1 + n × Unif()      //  Unif() returns a uniformly distributed

                                                    //  U(0,1) variate each time it is called.

                   y*(i) = y(j)

              }

              T*(k) = T(y*)

          }

 

The beautiful simplicity of bootstrapping is now apparent. The resampling is trivially easy. The step that produces T*(k) invokes the procedure that produced T from y, only y is replaced by y*. The key point here is that no matter how elaborate the original procedure was to produce T, we will already have it available, as we must have set it up in order to calculate T = T(y) in the first place. The bootstrap procedure simply calls it a further B times.

 

Example 13:  Use bootstrapping to produce 100 bootstrap versions of  of Exercise 11. Compare these with the confidence intervals produced for  using the asymptotic normality theory. Gamma Bootstrap

 

Produce confidence intervals for the waiting time in the queue using bootstrapping. Again compare these results with those produced by asymptotic theory.                      □

 

Example 13½: Use bootstrapping to produce bootstrap estimates of the parameters  in the logistic regression model for the Vaso Constriction Data.                                □

 

 

 

 

10.     Comparing Samples Using the Basic Bootstrap

 

Next we consider the problem where we have two samples of observations Y and Z and we wish to know if they have been drawn from the same or different distributions. We consider how the basic bootstrap provides a convenient way of answering this question.

 

To illustrate the ideas involved we consider the simple situation where we have calculated the same statistic from each of the samples Y and Z. This statistic might be the sample mean or sample variance say. We shall call this statistic S and denote its values calculated from the two samples by S(Y) and S(Z). An obvious statistic to use for the comparison, which we call the comparator statistic, is the difference . We therefore need the null distribution of T, corresponding to when Y and Z have been drawn from the same distribution. This null situation is depicted in Figure 10

 

Figure 10: Calculation of a Comparator Statistic

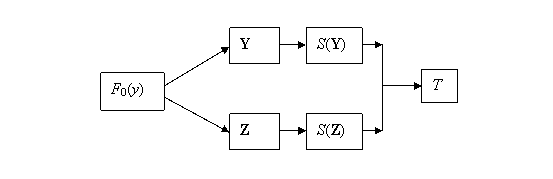
The procedure for producing a bootstrap version of T under the (null) assumption that the two samples are drawn from the same distribution is simple. We obtain bootstrap samples Y* and Z* from just one of the samples Y say. The bootstrap process is given in Figure 11. In the Figure  is the EDF constructed from Y. Alternatively the EDF  of Z, or perhaps even better, the EDF  of the two samples Y and Z when they are combined, could be used.

 

The test follows the standard test procedure. We calculate the p–value of the original comparator statistic T relative to the bootstrap EDF of the {Ti*}. The null hypothesis that the two samples Y and Z are drawn from the same distribution is then rejected if the p–value is too small.

 

Figure 11: Bootstrap Comparison of Two Samples

 

 

 

 

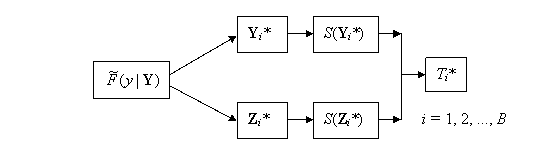
Example 14: Consider the data given in Law and Kelton (1991) recording the results of a simulation experiment comparing the costs of five different inventory policies. Five simulation runs were made for each of the five policies. The cost of running the inventory was recorded in each run and these results are reproduced in Table 1, together with the means obtained using each policy. Use bootstrapping to see if there are any significant differences between the five means.       Law and Kelton EG    

 

Table 1 (Law and Kelton Table 10.5):

Average cost per month for five replicates of each of five inventory policies.

 

 

Average cost in Run

Replicate j

Policy #1

Policy #2

Policy #3

Policy #4

Policy #5

1

126.97

118.21

120.77

131.64

141.09

2

124.31

120.22

129.32

137.07

143.86

3

126.68

122.45

120.61

129.91

144.30

4

122.66

122.68

123.65

129.97

141.72

5

127.23

119.40

127.34

131.08

142.61

Mean

125.57

120.59

124.34

131.93

142.72

                                                                                                                                □

 

11.     The Parametric Bootstrap

 

The previous discussion has considered the use of the basic bootstrap. There is a second method of bootstrapping which is unfairly sometimes considered to be less effective. This view arises probably because the problems where it can be used are similar to those of the basic bootstrap, but where it might be less accurate.  However it can be advantageous in certain specific situations when we are comparing models. We will discuss these problems in Section 13. but before doing so we need to describe how the parametric bootstrap works.

 

Suppose we have fitted a parametric model to data. If the parametric model is the correct one and describes the form of the data accurately, then the fitted parametric model will be a close representation of the unknown true parametric model. We can therefore generate bootstrap samples not by resampling from the original data, but by sampling from the fitted parametric model. This is called the parametric bootstrap.

 

The basic process is depicted in Figure 12. It will be seen that the method is identical in structure to the basic bootstrap. (Compare Figure 12 with Figure 8.) The only difference is that in the parametric version one has to generate samples from a given parametric distribution, like the gamma say. A method has to be available for doing this. As was seen in Exercise 9 the inverse transform method is one convenient way for doing this.

 

Figure 12: Parametric Bootstrap Process

 

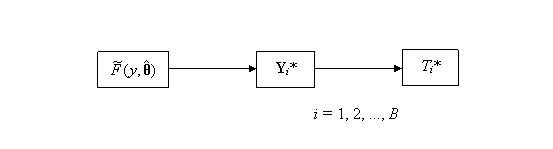
Example 15: Consider the queueing example where we have already used asymptotic theory and the basic bootstrap to analyse the effect of estimated parameter uncertainty. Repeat the exercise but now use the parametric bootstrap instead of the basic bootstrap.  ParametricBS-GammaEG                                                                   □

 

At first sight the parametric bootstrap does not seem to be a particularly good idea because it adds an extra layer of uncertainty into the process, requiring selection of a model that may or may not be right.

 

However there are situations where its use is advantageous and we discuss one in the next section.

 

12      Goodness of Fit Testing

 

12.1 Classical Goodness of Fit

 

We consider the natural question: Does the model that we have fitted actually fit the data very well? For instance in Exercise 11 (at the end of Section 5) we fitted a gamma distribution to toll booth service time data, but does the fitted gamma distribution capture the characteristics of the data properly?

 

The classical way to answer this question is to use a goodness of fit test (GOF test). A very popular test is the chi-squared goodness of fit test. The main reason for its popularity is that it is relatively easy to implement. The test statistic is easy to calculate and moreover it has a known chi-squared distribution, under the null, which makes critical values easy to obtain.

 

However the chi-squared test has two obvious weaknesses. It is actually not all that powerful, and it has a certain subjective element because the user has to divide the data into groups of her/his own choosing.

 

The best general GOF tests directly compare the EDF with the fitted CDF. Such tests are called EDF goodness of fit tests. In the past the Kolmogorov-Smirnov test has been the most popular, but the Cramér - von Mises test and the Anderson - Darling test, defined below, are generally more powerful and should be used in preference. The trouble with these tests is that, because of their sensitivity, their critical values are very dependent on the model being tested, and on whether the model has been fitted (with parameters having to be estimated in consequence). This means that different tables of test values are required for different models (see d’Agostino and Stephens, 1986).

 

First we describe EDF tests in more detail. Applying the Fundamental Theorem of Section 7, we see that a natural way to test if a sample has been drawn from the distribution with CDF F0(y), is to compare  with F0(y) by looking at some quantity involving the difference  – F0(y). Such an EDF test statistic typically has the form

 

                        .

 

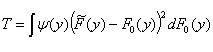Here y(y) is a weighting function. Special cases are the Cramér-von Mises test statistic:

                       

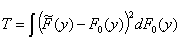
where y(y) = 1, and the Anderson-Darling test statistic:

 

                       

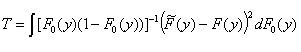
where y(y) = [F0(y)(1 – F0 (x))]-1 .

 

At first sight such GOF test statistic seem difficult to calculate involving a nasty integration. In fact things are much more straightforward than this. For example, the Anderson-Darling statistic (which is conventionally denoted by A2) is easily calculated using the equivalent formula

 

                       

 

where  is the value of the fitted CDF at the ith ordered observation.

 

The basic idea in using a goodness of fit test statistic is as follows. When the sample has really been drawn from F0(y) then the value of the test statistic will be small. This follows from the Fundamental Theorem of Section 7 which guarantees that  will be close in value to F0(y) across the range of possible y values. Thus T will be small. Nevertheless because the test statistic is a random quantity, it will have some variability according to a null distribution depending on the sample size n. If the null distribution is known then we can assess an observed value of T against this distribution. If the sample is drawn from a distribution different from F0(y) then the T will be large. Statistically, what is conventionally called its p - value will then be small, indicating that the distribution has not been drawn from the supposed null distribution.

 

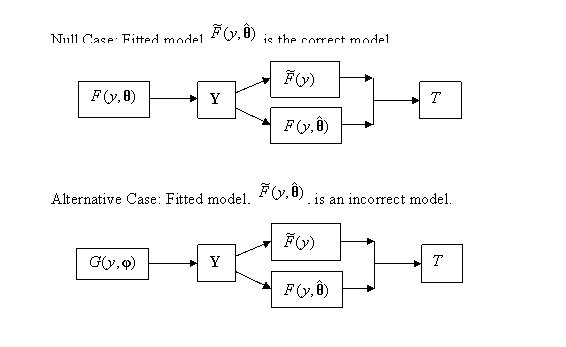
Figure 13 illustrates the process involved in calculating a GOF test statistic for the parametric case. Two cases are shown. In both cases the distribution from which Y has been drawn is assumed to be , but where  is unknown; thus in each case  has been fitted to the random sample Y giving the ML estimate  of . However in the first case  is the correct model. Thus  will be the EDF of a sample drawn from  which will therefore converge to this distribution. In the second case the true model, , is different from , and may even involve a set of parameters  that is different from .  Thus the EDF  in this second case will not converge to , but to . Thus in the second case, T, which is a measure of the difference between the two, will be larger than in the first case.

 

The null situation is the first case where we are fitting the correct model. We need to calculate the distribution of T for this case. A complication arises because the difference between  and  is smaller than the difference between  and the unknown true. This is because the fitted distribution  will follow the sample more closely than  because it has been fitted to the sample. This has to be allowed for in calculating the null distribution of the test statistic.

 

 

 

 

 

Figure 13: Process Underlying the Calculation of a GOF Test, T

 

 

 

It will be seen that the GOF test hinges on being able to calculate the null distribution. This is a big issue and has meant that many potentially powerful test statistics, like the Cramér - von Mises, have not been fully utilized in practice because the null distribution is difficult to obtain.

 

In the next subsection we show how resampling provides a simple and accurate way of resolving this problem.

 

12.2.  Bootstrapping a GOF statistic

 

The null case calculation of the GOF statistic depicted in Figure 13 is identical to that of Figure 7. Thus if we could obtain many values of T using this process then the EDF of the Ti will converge to the CDF of T.  This is almost certainly too expensive or impractical to do. However we can get a close approximation by simply replacing the unknown  by its MLE . This is precisely the parametric bootstrap process as given in Figure 12.

 

All being well  will be close in value to . Thus the distributional properties of the  will be close to those of a set of obtained under the null case calculation of Figure 13.

 

The parametric bootstrap method as it applies to a GOF statistic is illustrated in more detail in Figure 14, where  is the EDF of the bootstrap sample , and  is the bootstrap MLE of obtained from the bootstrap sample

 

Example 16: Examine whether the gamma model is a good fit to the toll booth data. Examine also whether the normal model is a good fit to the toll booth data. Use the Anderson-Darling goodness of fit statistic A2, previously given.

Gamma Fit Toll Booth Data          Normal Fit Toll Booth Data                              □

 

 

 

Figure 14: Bootstrap Process to Calculation the Distribution of a GOF Test, T

 

 

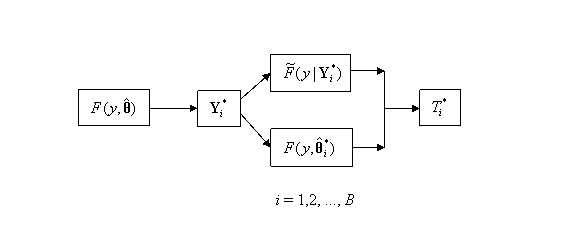
13      Comparison of Different Models; Model Selection

 

We consider the situation where we have a number of alternative models that might be fitted to a set of data, and we wish to choose which model is the best fit. We shall only discuss the regression modelling case where the data are of the form

 

                         

 

and  but where it is not clear which of the components of  are required in the best model. A common example is in multiple linear regression where Y depends on a number of factors

 

                       

 

but it is not clear which ones are important. Here a decision has to be taken on each factor as to whether to include it or not. Assuming that the constant θ0 is always fitted there are  different models with precisely k factors, k = 0, 1, ..., M, making a total of 2M different possible models in all. Krzanowski (1998) gives three quantities that measure how well a given model fits:

 

          (i) Residual Mean Square RMSk = SSEk-1/(n-k), where SSEk-1 is the residual sum of squares when there are k – 1 factors in the model.

          (ii) Coefficient of Determination , where CSS is the total sum of squares corrected for the mean.

 

          (iii) Mallow’s Statistic , where RSSk is the regression sum of squares from fitting k - 1 factors and RMSM+1 is the residual mean square from fitting the full model.

 

We do not discuss the methodology here except to note that when M is large then a systematic search through all possible models will be computationally expensive.

 

Less computationally expensive methods are the forward or backward elimination methods. Interesting cross-validation methods are discussed by Davison and Hinkley (1997). Some very effective methods are discussed by Goldsman and Nelson (Chapter 8,  Banks, 1998).

 

We shall not discuss the pros and cons of model selection, but look at how bootstrapping can be of use. Suppose that we have selected the ‘best’ model according to one of the above criteria. How reliable is this choice? Put another way what degree of confidence can we place on the choice made? Bootstrapping provides a very effective way of answering this question.

 

Example 17: The following data came from tests a cement manufacturer did on the amount of heat Y their cement gave off when setting, and how it depended on the amount it contained of four chemical compounds : X1, X2, X3, X4. The question is which of these compounds has the most influence? This is studied in  Cement Data                                                                                                                                          □

 

This completes our discussion of some of the basic problems that regularly occur in modelling.

 

 

14      Final Comments

 

This course has reviewed the process of constructing and fitting a statistical model to data whether this data arises from study of a real system or from a simulation.

 

The classical approach using the method of maximum likelihood has been described for fitting the model.

 

Two approaches for assessing the variability of fitted parameters have been discussed:

              (i) The classical approach using asymptotic normality theory.

              (ii) Bootstrap resampling.

 

Examples have been drawn mainly from regression and ANOVA applications. These have been for illustration only and I have not attempted to survey the range of statistical models likely to be encountered in practice, where typically different aspects of modelling need to be brought together. Krzanowski (1998) gives a very comprehensive but at the same time very accessible survey of the different types of situation commonly encountered. For instance, Krzanowski’s Example 6.1 gives data relating to factors affecting the risk of heart problems: social class, smoking, alcohol and so on. The data is ‘binary response’ data (i.e a patient reporting some form of ‘heart trouble’ or not). The factors are categorical (for example alcohol is coded as someone who drinks or someone who does not). The required model is therefore a logisitc regression model but with a linear predictor involving the categorical factors. Though this example has not been discussed explicitly in this course, all the elements needed to analyse it using either classical or bootstrap methods have been considered, and despite its apparent complexity, this model is quite capable of being tackled straightforwardly using the methods of this course.

 

In fact the spreadsheets given for the examples in this course use a number of VBA macros that enable various commonly occurring analyses to be carried out. These macros have been designed to be sufficiently flexible and accessible to be used in other applications and you are encouraged to make use of them in this way.

 

 

References

 

Banks, J. (1998). Handbook of Simulation. New York: Wiley.

 

Chernick, M.R. (1999). Bootstrap Methods, A Practitioner's Guide. New York: Wiley.

 

D'Agostino, R.B. and Stephens, M.A. (1986). Goodness of Fit Techniques. New York: Marcel Dekker.

 

Davison, A.C. and Hinkley, D.V. (1997). Bootstrap Methods and their Application. Cambridge: Cambridge University Press.

 

Krzanowski, W.J. (1998). An Introduction to Statistical Modelling. London: Arnold.

 

Law, A.M. and Kelton, W.D. (1991). Simulation Modeling and analysis, 2nd Ed., New York: McGraw-Hill.

 

Urban Hjorth, J.S. (1994). Computer Intensive Statistical Methods. London: Chapman & Hall.