Forecasting

3. Basic Forecasting Methods

In this chapter we suppose that we are currently at time t and that we wish to use the data up to this time, ie Y₁, Y₂, ..., Y_t-1, Y_t, to make forecasts F_t+1, F_t+2, ..., F_t+m of future values of Y.

The methods to be considered are conventionally regarded as being divided in two groups: (i) averaging methods and (ii) exponential smoothing methods.

Though it is convenient to follow this convention it is important to realise at the outset that this distinction is artificial in that all the methods in this chapter are methods based on averages. They are thus all similar to the moving averages considered in the last chapter. The difference is that the averages are used for forecasting rather than for describing past data.

This point of potential confusion is made worse by the use of the name 'exponential smoothing' for the second group. These methods are also based on weighted averages, where the weights decay in an exponential way from the most recent to the most distant data point. The term smoothing is being used simply to indicate that this weighted average smoothes the data irregularities. Thus, though the term smoothing here is used in the same sense as previously, the smoothing is being carried out in a different context from that used in the previous chapter.

3.1 Averaging Methods

The moving average forecast of order k , which we write as MA(k), is defined as

.

This forecast is only useful if the data does not contain a trend-cycle or a seasonal component. In other words the data must be stationary. Data is said to be stationary if Y_t, which is a random variable, has a probability distribution that does not depend on t.

A convenient way of implementing this forecast is to note that

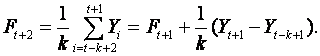
This is known as an updating formula as it allows a forecast value to be obtained from the previous forecast value by a simpler calculation than using the defining expression.

The only point of note is that moving average forecasts give a progressively smoother forecast as the order increases, but a moving average of large order will be slow to respond to real but rapid changes. Thus, in choosing k, a balance has to be drawn between smoothness and ensuring that this lag is not unacceptably large.

3.2 Single Exponential Smoothing

The single exponential forecast or single exponential smoothing (SES) is defined as

F_t+1 = αY_t + (1 − α)F_t,

where α is a given weight value to be selected subject to 0 < α < 1. Thus F_t+1 is the weighted average of the current observation, Y_t, with the forecast, F_t, made at the previous time point t − 1.

Repeated application of the formula yields

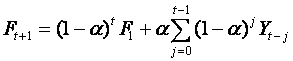
showing that the dependence of the current forecast on Y_t, Y_t-1, Y_t-2, ...falls away in an exponential way. The rate at which this dependence falls away is controlled by α. The larger the value of α the quicker does the dependence on previous values fall away.

SES needs to be initialized. A simple choice is to use

F₂ = Y₁.

Other values are possible, but we shall not agonise over this too much as we are more concerned with the behaviour of the forecast once it has been in use for a while.

Exercise 3.1: Employ SES for the Shampoo Data.

1. Set up α in a named cell.

2. Plot the Y_t and the SES.

3. Calculate also the MSE of the SES from Y.

4. Try different values of α. Use Solver to minimize the MSE by varying α.

[Web: Shampoo Data ].

3.3 Holt's Linear Exponential Smoothing (LES)

This is an extension of exponential smoothing to take into account a possible linear trend. There are two smoothing constants α and β. The equations are:

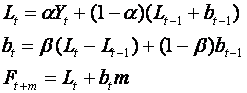
Here L_t and b_t are respectively (exponentially smoothed) estimates of the level and linear trend of the series at time t, whilst F_t+m is the linear forecast from t onwards.

Initial estimates are needed for L₁ and b₁. Simple choices are

L₁ = Y₁ and b₁ = 0.

If however zero is atypical of the initial slope then a more careful estimate of the slope may be needed to ensure that the initial forecasts are not badly out.

Exercise 3.2: Employ LES for the Shampoo Data.

1. Set up α and β in a named cells.

2. Plot the Y_t and the LES.

3. Calculate also the MSE of the LES from Y.

4. Try different values of α and β. Use Solver to minimize the MSE by varying α and β.

5. Make sure that you arrange the calculations in a neat block of cells with the Y_t in a column on the left. This will allow you to use LES on different data sets. This will be useful later on in the Unit.

[Web: Shampoo Data ].

3.4 Holt-Winter's Method

This is an extension of Holt's LES to take into account seasonality. There are two versions, with the multiplicative the more widely used.

3.4.1 Holt-Winter's Method, Multiplicative Seasonality

The equations are

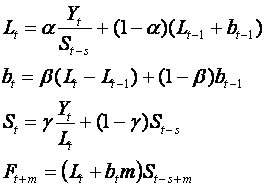
where s is the number of periods in one cycle of seasons e.g. number of months or quarters in a year.

To initialize we need one complete cycle of data, i.e. s values. Then set

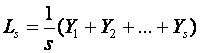
To initialize trend we use s + k time periods.

.

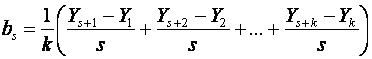If the series is long enough then a good choice is to make k = s so that two complete cycles are used. However we can, at a pinch, use k = 1.

Initial seasonal indices can be taken as

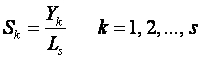
The parameters α, β, γ should lie in the interval (0, 1), and can be selected by minimising MAD, MSE or MAPE.

3.4.2 Holt-Winter's Method, Additive Seasonality

The equations are

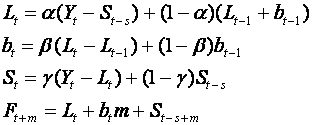
where s is the number of periods in one cycle.

The initial values of L_s and b_s can be as in the multiplicative case. The initial seasonal indices can be taken as

.

The parameters α, β, γ should lie in the interval (0, 1), and can again be selected by minimising MAD, MSE or MAPE.

Exercise 3.3: Apply Holt-Winter's forecasting to the Airline Passengers Data.

1. Follow the same arrangement as in Exercise 3.2.

2. Compare your results for Holt-Winter's methods with those for SES and for LES.

[Web: Airline Passengers Data ]