Bootstrap Resampling Methods

 

Part II

 

3.  Random Variables

 

The key concept of all statistics is the random variable. Strictly a random variable is a function whose domain is a sample space over which an associated probability distribution is defined. From a practical viewpoint a random variable is simply a quantity that one can observe many times but that takes different values each time it is observed in an unpredictable, random way. These values however will follow a probability distribution. The probability distribution is thus the defining property of a random variable. Thus, given a random variable, the immediate and only question one can, and should always ask is: What is its distribution?

 

We denote a random variable by an upper case letter X (Y, Z etc.). An observed value of such a random variable will be denoted by a lower case letter x (y, z etc).

 

In view of the above discussion, given a random variable, one should immediately think of the range of possible values that it can take and its probability distribution over this range.

 

The definition of most statistical probability distributions involves parameters. Such a probability distribution is completely fixed once the parameter values are known. Well known parametric probability distributions are the normal, exponential, gamma, binomial and Poisson.

 

A probability distribution is usually either discrete or continuous. A discrete distribution takes a specific set of values, typically the integers 0, 1, 2,…. Each value i has a given probability pi of occurring. This set of probabilities is called its probability mass function.

 

A continuous random variable, as its name implies, takes a continuous range of values for example all y ≥ 0. One way of defining its distribution is to give its probability density function (pdf), typically written as f(y). The pdf is not a probability, however it can be used to form a probability increment.  This is a good way to view the pdf.

 

An alternative way of defining a probability distribution, which applies to either a discrete or continuous distribution, is to give its cumulative distribution function (cdf).

 

4.  Fitting Parametric Distributions to Random Samples; Input Modelling

 

Random samples are the simplest data sets that are encountered. A random sample is just a set of n independent and identically distributed observations (of a random variable). We write it as Y = {Y1, Y2, … Yn,} where each Yi represents one of the observations.

 

Exercise 9: Generate random samples from

(i)                  the normal distribution . Normal Var Generator

(ii)                the gamma distribution .  Gamma Var Generator

 

A basic problem is when we wish to fit a parametric distribution to a random sample. This problem is an elementary form of modelling called input modelling.

 

Example 1 (continued): Suppose we are modelling a queueing system where service times are expected to have a gamma distribution and we have some actual data of the service times of a number of customers from which we wish to estimate the parameters of the distribution. This is an example of the input modelling problem. If we can estimate the parameters of the distribution, we will have identified the distribution completely and can then use it to study the characteristics of the system employing either queueing theory or simulation.                                                          □

 

To fit a distribution, a method of estimating the parameters is needed. The best method by far is the method of maximum likelihood (ML). The resulting estimates of parameters, which as we shall see shortly possess a number of very desirable properties, are called maximum likelihood estimates (MLEs). ML estimation is a completely general method that applies not only to input modelling problems but to all parametric estimation problems. We describe the method next.

 

 

5.  Maximum Likelihood Estimation

 

Suppose Y = {Y1, Y2, …, Yn} is a set of observations where the ith observation, Yi, is a random variable drawn from the continuous distribution with pdf fi(y, θ) (i = 1, 2, …, n). The subscript i indicates that the distributions of the yi can all be different.

 

Example 7: Suppose Yi ~ N(μ, σ 2) all i. In this case

                                                                                (9)

so that the observations are identically distributed. The set of observations is therefore a random sample in this case.                                                                                   □

 

Example 8: Suppose Yi ~ , i = 1, 2, ..., n. In this case one often writes

 

                                                                                                     (10)

where

 

                                                                                                    (11)

 

is called the regression function, and

 

                             ~ N(0, σ 2)                                                                              (2 bis)

 

can be thought of as an error term, or a perturbation affecting proper observation of the regression function.                                                                                             □

 

In the example, the regression function is linear in both the parameters , and in the explanatory variable x. In general the regression function can be highly nonlinear in both the parameters and in the explanatory variables. Study of nonlinear regression models forms a major part of this course.

 

In Example 8, the pdf of Yi is

 

                             .                                        (12)

 

Thus Y is not a random sample in this case, because the observations are not all identically distributed. However ML estimation still works in this case.

 

We now describe the method. Suppose that y = {y1, y2, …, yn} is a sampled value of Y = {Y1, Y2, …, Yn}. Then we write down the joint distribution of Y evaluated at the sampled value y as:

 

                             .                                        (13)

 

This expression, treated as a function of θ, is called the called the likelihood (of the sampled value y). The logarithm:

 

                 (14)

 

is called the loglikelihood.

 

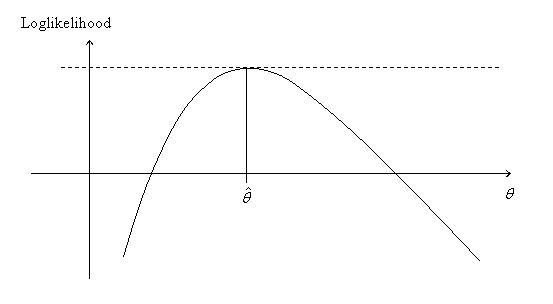
The ML estimate, , is that value of which maximizes the loglikelihood.

 

The MLE is illustrated in Figure 5 in the one parameter case. In some cases the maximum can be obtained explicitly as the solution of the vector equation

 

                                                                                                             (15)

 

which identifies the stationary points of the likelihood. The maximum is often obtained at such a stationary point. This equation is called the likelihood equation. The MLE illustrated in Figure 5 corresponds to a stationary point.

 

Figure 5.   The Maximum Likelihood Estimator

 

 

In certain situations, and this includes some well known standard ones, the likelihood equations can be solved to give the ML estimators explicitly. This is preferable when it can be done. However in general the likelihood equations are not very tractable. Then a much more practical approach is to obtain the maximum using a numerical search method.

 

There are two immediate and important points to realise in using the ML method.

 

          (i) An expression for the likelihood needs to be written down using (13) or (14).

          (ii) A method has to be available for carrying out the optimization.

 

We illustrate (i) with some examples.

 

Example 9: Write down the likelihood and loglikelihood for

              (i) The sample of Example 7

              (ii) The sample of Example 8

              (iii) A sample of observations with the Bernoulli distributions (8).

               (iv) The sample of Example 3                     

              Likelihood Examples                                                                                   □

 

We now consider the second point, which concerns how to find the maximum of the likelihood. There exists a number of powerful numerical optimizing methods but these can be laborious to set up. Most statistical packages include optimizers. Such optimizers are fine when they work, but can be frustrating when they fail, or if the problem you are tackling has features that they have not been designed to handle.

 

A more flexible alternative is to use a direct search method like the Nelder-Mead method. This is discussed in more detail here in the following reference here:    Nelder Mead.

 

Exercise 10: NelderMeadDemo This is a VBA implementation of the Nelder-Mead Algorithm. Insert a function of your own to be optimized and see if it finds the optimum correctly.

 

Watchpoint: Check whether an optimizer minimizes or maximizes the objective. Nelder Mead usually does function minimization.                                                    □

 

Exercise 11: The following is a (random) sample of 47 observed times (in seconds) for vehicles to pay the toll at a booth when crossing the Severn River Bridge. Use the Nelder-Mead method to fit the gamma distribution G(α, β) to this data using the method of maximum likelihood. Gamma MLE

 

Watchpoints: Write down the loglikelihood for this example yourself, and check that you know how it is incorporated in the spreadsheet.                                                    □

 

 

 

 

 

 

6.  Accuracy of ML Estimators

 

A natural question to ask of an MLE is: How accurate is it? Now an MLE, being just a function of the sample, is a statistic, and so is a random variable. Thus the question is answered once we know its distribution.

 

An important property of the MLE, , is that its asymptotic probability distribution is known to be normal. In fact it is known that, as the sample size n → ∞,

 

                              ~                                                                       (16)

 

where is the unknown true parameter value and the variance has the form

 

                             ,                                                                       (17)

where

                                                                                               (18)

is called the information matrix. Thus the asymptotic variance of  is the inverse of the information matrix evaluated at . Its value cannot be computed precisely as it depends on the unknown , but it can be approximated by

 

                             .                                                                           (19)

 

The expectation in the definition of  is with respect to the joint distribution of Y and this expectation can be hard to evaluate. In practice the approximation

 

                              '                                                 (20)

 

where we replace the information matrix by its sample analogue, called the observed information, is quite adequate. Practical experience indicates that it tends to give a better indication of the actual variability of the MLE. Thus the working version of (16) is

 

                              ~                                                                              (21)

 

The second derivative of the loglikelihood, , that appears in the expression for  is called the Hessian (of L). It measures the rate of change of the derivative of the loglikelihood. This is essentially the curvature of the loglikelihood. Thus it will be seen that the variance is simply the inverse of the magnitude of this curvature at the stationary point.

 

Though easier to calculate than the expectation, the expression  can still be very messy to evaluate analytically. Again it is usually much easier to calculate this numerically using a finite-difference formula for the second derivatives. The expression is a matrix of course, and the variance-covariance matrix of the MLE is the negative of its inverse. A numerical procedure is needed for this inversion.

 

The way that (21) is typically used is to provide confidence intervals. For example a (1-α)100% confidence interval for the coefficient θ1 is

 

                                                                                                      (22)

 

where is the upper 100α/2 percentage point of the standard normal distribution.

 

Often we are interested not in θ directly, but some arbitrary, but given function of θ, g(θ) say. ML estimation has the attractive general invariant property that the MLE of

g(θ) is

                             .                                                                                    (23)

 

An approximate (1-α)100% confidence interval for g(θ) is then

 

                                                             (24)

 

In this formula the first derivative of g(θ) is required. If this is not tractable to obtain analytically then, as with the evaluation of the information matrix, it should be obtained numerically using a finite-difference calculation.

 

Summarising it will be seen that we need to

 

     (i)      Formulate a statistical model of the data to be examined. (The data may or may not have been already collected. The data might arise from observation of a real situation, but it might just as well have been obtained from a simulation.)

 

     (ii)     Write down an expression for the loglikelihood of the data, identifying the parameters to be estimated.

 

     (iii)    Use this in a (Nelder-Mead say) numerical optimization of the loglikelihood.

 

     (iv)    Use the optimized parameter values as estimates for the quantities of interest.

 

     (v)          Calculate confidence intervals for these quantities.

 

Example 10: Suppose that the gamma distribution  fitted to the toll booth data of Exercise 11 is used as the service distribution in the design of an M/G/1 queue. Suppose the interarrival time distribution is known to be exponential with pdf

 

                                                                                              (25)

 

but a range of possible values for the arrival rate, λ, needs to be considered.

 

Under these assumptions the steady state mean waiting time in the queue is known to be

                             .                                                        (26)

 

Plot a graph of the mean waiting time  for the queue for 0 < λ < 0.1 (per second), assuming that the service time distribution is gamma: . Add 95% confidence intervals to this graph to take into account the uncertainty concerning  because estimated values  have been used. Gamma MLE              □

 

Example 11: Analyse the Moroccan Data of Example 3. Fit the model

 

                      i = 1,2, .... 32

 

where xi is the age group of the ith observation,

 

                   ,

 

and  ~ N(0, θ12).                                               Regression Fit Morocco Data             □

 

 

The previous two examples contain all the key steps in the fitting of a statistical model to data. Both examples involve regression situations. However the method extends easily to other situations like the Bernoulli model of Equation (8).

 

 

Exercise 11½: Analyse the Vaso Constriction Data by fitting the Bernoulli model of Equation (8) using ML estimation.                                                                              □

 

 

There are usually additional analyses that are then subsequently required such as model validation and selection and sensitivity analyses. We will be discussing these in Part III. Before turning to these we shall introduce a method of sensitivity analysis using what are sometimes referred to as computer intensive methods.

 

Our discussion so far has relied heavily on the classic asymptotic theory of MLE’s. The formulas based on this classical approach are useful to calculate, but only become accurate with increasing sample size. With existing computing power, computer intensive methods can often be used instead to assess the variability of estimators.

 

Experience (and theory) has shown these will often give better results in general for small sample sizes. Moreover this alternative approach is usually much easier to implement than the classical methodology. The method is called bootstrap resampling, or simply resampling.

 

Resampling hinges on the properties of the empirical distribution function (EDF) which we need to discuss first, and this is what we shall start with in Part III.