Experimental Design and Analysis

Part IV Experimental Design and Analysis of Linear Models

One of the most useful statistical models is the ‘Linear Model’. We encountered it in Example 2.2 of Part I. Here in Part IV of Experimental Design and Analysis, we discuss its form in more detail and examine how to fit it to data, including simulation data. We then give an introduction to how simulation experiments using this metamodel should be designed. In complex simulations, a well designed experiment is not just a luxury, but can mean the difference between a project that is successfully carried out in a timely way, and one that that is impossible to carry out in a realistic time-frame.

14 Linear Regression Metamodels.

Each observation is assumed to take the form (Y, X₁, X₂, … X_P) where Y the output of interest, is assumed to be dependent on P decision or explanatory, variables X_j, j = 1, 2, …, P, often called factors. [Note that in this section we use the notation P for the number of factors, rather than the M previously used,] Assume there are n observations. In a simulation experiment this will have been obtained from n runs. In the linear (regression) model it is assumed that:

. (14.1)

where Y_i is the ith observation and X_ij is the observed value of the jth factor in the ith observation. It is usual to assume that the errors are mutually independent and normally distributed:

~ . (14.2)

The coefficients , j = 0, 1, …, P are assumed unknown and have to be estimated from the data. This is usually termed ‘fitting’ the model. We shall discuss this process in the next section. Notice that these coefficients appear linearly in (14.1), which is why the model is termed ‘linear’. At first sight it might appear that the factors also enter linearly, but this is not necessarily so. In the simplest case, where the factors are all distinct and quantitative (as opposed to being qualitative), the factors can indeed be regarded as appearing linearly, as each variable is present linearly and in its own right. In the general literature on the statistical design of experiments such a model is called a main-effects model.

However there is no difficulty in including quadratic, or more general second-order effects factor effects such as X₁² or X₁X₂. Thus the second-order model

(14.3)

is still a linear model. Second order effects like X₁X₂ are often called two-way interactions. Indeed much of the statistical literature on the linear model develops the theory in terms of two-way interactions, rather than in terms of second-order regression models, to the extent that the first time reader may not realise that the two forms of model are identical. A curious, and rather unsatisfactory, aspect of the interaction approach is that often the pure quadratic terms X_i² are omitted from consideration. It would seem inadvisable not to at least consider the possible effect of pure quadratic terms if two-way interactions are expected, or turn out to be important.

In complex simulations a simple initial approach is to assume that a linear model can be fitted to the results of a set of simulation runs, where we are free to select the factor values to be used in each of the simulation runs. Badly chosen factor values can result in difficulties in fitting the assumed linear model. Thus we may end up with a situation where the coefficients are not accurately estimated or worse still where some cannot be estimated at all from the simulation runs made. To make this more precise, we first summarize how the coefficients can be estimated.

When there are a large number of explanatory variables it is useful to use vector notation. We can write (14.1) either in the partial vector form

Y_i = X_ib+ e_i, i = 1, 2, ..., n (14.4)

where X_i = (1, X_i1, X_i2, , X_iP) is a row vector, and the unknown coefficients are written as the column vector

b = (b₀, b₁, ..., b_P)^T (14.5)

(where the superscript T denotes the transpose), or in the full vector form

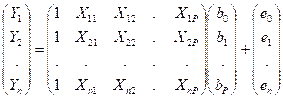(14.6)

i.e.

Y = Xb + e (14.7)

The values of the explanatory variables written in the matrix form, X, is called the design matrix. In classical regression this is usually taken to be non random. This is in line with our simulation viewpoint that the explanatory variables are decision variables who values we can choose and fix.

Exercise 14.1: Identify the observations Y and the design matrix X for the Fire Rescue Service Simulation Data. ANOVAFireRescueServiceEG.xls

15 Fitting and Assessing the Linear Model

15.1 Least Squares Estimation

The coefficients b are assumed unknown. They have to be estimated from the observations. The most commonly suggested method of estimation is that of least squares (LS). A good description of least squares estimation at a reasonably accessible level is Wetherill (1981). A good Web reference is http://www.statsoftinc.com/textbook/stmulreg.html. We summarize the method here.

Least squares (LS) estimation obtains b by minimizing the sum of squares

(15.1)

with respect to b. An arguably more statistically satisfactory method is that of maximum likelihood, introduced in Part II. This latter method requires an explicit form to be assumed for the distribution of , such as the normal distribution of (14.2), whereas least squares does not require this assumption. In the special case where the errors are assumed to be normally distributed then least squares and maximum likelihood methods are in fact essentially equivalent.

The LS estimator of b is

= (X^TX)⁻¹X^TY. (15.2)

The least squares method does not yield an estimate of , the variance of , and usually a quite different idea, that of unbiasedness, is invoked to provide an estimate. In contrast the maximum likelihood method provides an estimate directly as

(15.3)

where

. (15.4)

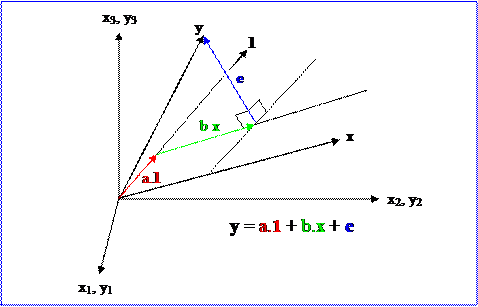
Geometric Interpretation of fitting

15.2 ANOVA

The accuracy and effectiveness of the linear model in explaining the dependence of observed output Y on the explanatory variables can be neatly described by carrying out an analysis of variance. This is done as follows.

The total sum of squares (corrected for the overall mean) is

(15.5)

where . This decomposes into

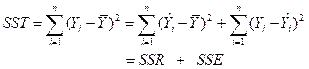(15.6)

where

(15.7)

is called the regression sum of squares. This measures the reduction in total sum of squares due to fitting the terms involving the explanatory variables. The other term

(15.8)

is called the (minimized) residual or error sum of squares and gives the variance of the total sum of squares not explained by the explanatory variables.

The sample correlation, , between the observations Y_i and the estimates can be calculated from the usual sample correlation formula and is called the multiple correlation coefficient. Its square turns out to be

. (15.9)

This is called the coefficient of determination. R² is a measure of the proportion of the variance of the Y's accounted for by the explanatory variables.

The sums of squares each have an associated number of degrees of freedom and a corresponding mean square

(i) For SST: dfT = n − 1, and MST = SST/dfT

(ii) for SSR: dfR = P (i.e. the # of coefficients − 1) and MSR = SSR/dfR

(iii) For SSE: dfE = n − P − 1 and MSE =SSE/dfE

Thus we have

dfT = dfR + dfE. (15.10)

Under the assumption that the errors, e_i, are all independent and normally distributed, the distributional properties of all the quantities just discussed are well known.

If in fact the b_i i = 1,2,..., P are zero so that the explanatory variables are ineffective then the quantity

(15.11)

has the F-distribution with P and (n − P − 1) degrees of freedom. If the b_i are non zero the F tends to be larger.

These calculations are conventionally set out in the following analysis of variance (ANOVA) table

—————————————————————————————————

Source Sum of df MS F P

Squares

—————————————————————————————————

Regression SSR P SSR/P MSR/MSE p-value

Error SSE (n − P − 1) SSE/(n − P − 1)

—————————————————————————————————

Total SST (n − 1)

—————————————————————————————————

Exercise 15.1: Carry out the ANOVA for Fire Rescue Service Simulation Data ANOVAFireRescueServiceEG.xls

15.3 Individual Coefficients

Either the coefficient of determination, R ², or the F - ratio gives an overall measure of the significance of the explanatory variables. If overall significance is established then it is natural to try to identify which of the explanatory variable is having the most effect. Individual coefficients can be tested in the presence of all the other explanatory variables relatively easily.

Again we assume that the errors e_i are N(0, σ²) variables. Then the covariance matrix of is given by

Var() = (X^TX)⁻¹σ². (15.12)

An alternative estimate of σ ² is given by the MSE:

. (15.13)

If the true value of b_i = 0, so that the explanatory variable is not effective, then it is known that

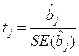(15.14)

where is the standard error of has the t-distribution with (n − P − 1) degrees of freedom.

The P-value of t_j i.e. Pr(T > |t_j|) where T is a random variable having the t-distribution with (n − p − 1) degrees of freedom can then be found.

Alternatively, and rather better, is to calculate a 100(1 − α)% confidence interval for the unknown true value of b_j as

± t(α/2). . (15.15)

Exercise 15.2: Identify and for the Fire Rescue Service Simulation Data.

ANOVAFireRescueServiceEG.xls

15.4 Selecting Important Coefficients

A simple method for identifying good possible models is to use bootstrapping. We generate B bootstrap samples of form (14.7). The simplest way to do this is to use parametric bootstrapping. Thus the ith bootstrap sample is

(15.16)

where each entry in the vector of errors , is a normally distributed variate sampled form the fitted error distribution .

For each bootstrap sample we estimate the coefficients using (15.2). Then for that sample we take as our best fitted model for that sample, that which includes just those coefficients b_j for which the corresponding t_j value is significantly different from zero.

It turns out , for an orthogonal design, that if the level of significance for testing each individual coefficient is taken as 91.7%, then overall, the method becomes equivalent to the criterion ‘choose that model for which the Mallows statistic C_p (introduced in Part III) is minimized’. We use this criterion even if the design is not orthogonal, as we are only interested in using bootstrapping to generate a set of ‘promising’ models that might be a good fit.

A method for choosing between these promising models is to calculate, using the original sample, the C_p statistic proposed by Mallows (1973) for each promising model. For a given model, m say, containing p - 1 of the full set of P factors (thus when we include the unknown constant, there are p unknown coefficients), C_p is defined as

where is the variance estimated by fitting the full model with P factors, and is the variance estimated from the model m. An alternative statistic is the Akaike Information Criterion (Akaike, 1970), which for the linear model reduces to

.

Asymptotically C_p and AIC have the same distribution. However C_p is perhaps more satisfactory for our purpose because of its ease of interpretation. Mallows (1973) shows that if the model m (with p - 1 factors) is satisfactory in the sense that it has no bias, then the expected value of C_p is close to p:

.

Thus once all important factors are included, C_p will increase linearly with p. However if not all important factors are included, the expected value of C_p will be larger than p. A simple selection method is therefore the following.

Bootstrap “Min C_p” Selection Method

(i) Consider each of the models of selected by the simple bootstrap analysis and for each model m calculate C_p(m).

(ii) Select as the best model that m for which C_p(m) is minimum, with the expectation that this model will be satisfactory if .

The advantageof this bootstrap method of selecting a model is that it avoids having to examine a potentially huge number of possible models, but considers a set of good models produced by the bootstrap process.

Exercise 15.2: Suggest a model for the Fire Rescue Service Simulation Data. ANOVAFireRescueServiceEG.xls

16 Prediction with the Linear Model

The linear model is a particularly simple form of regression model where the regression function, E(Y(X)), is linear in the parameters. This allows a simple application of the analysis of Section 15 to predict the expected value of Y, E(Y(X₀)), at any given value of the explanatory variables, X₀ = (1, X₀₁, X₀₂, , X_0p), using

. (16.1)

An estimate of the accuracy of this prediction is given by

, (16.2)

where can be estimated by either of (15.3) or by of (15.13).

Time is not explicitly involved in these formulas. Thus we are not using the word predict necessarily in the sense of forecasting the future. We use 'predict' only in the sense that the fitted regression model is used to estimate the value of regression function that corresponds to a particular set of values of the explanatory variables. If however one of the explanatory variable is time, t, then we can use linear regression as a forecasting tool.

17 Additional Explanatory Variables

In any regression model, one may consider introducing additional explanatory variables to explain more of the variability of Y. This is especially desirable when the error sum of squares, SSE is large compared with SSR after fitting the initial set of explanatory variables.

One useful type of additional variable to consider is what are called indicator variables. This arises when one wishes to include an explanatory variable that is categorical in form. A categorical variable is one that takes only a small set of distinct values.

For example suppose we have a categorical variable, W, taking just one of four values Low, Medium, High, Very High. If the effect of W on Y is predictable then it might be quite appropriate to assign the values 1, 2, 3, 4 to the categories Low, Medium, High, Very High and then account for the effect of W using just one coefficient a:

Y_i = b₀ + b₁X_i1 + b₂X_i2 +...+ b_p X_ip + aW + e_i, i = 1, 2, ..., n. (17.1)

However if the effect of each of the different possible values of the categorical variable on Y is not known then we can adopt the following different approach. If there are c categories then we introduce (c − 1) indicator variables. In the example we therefore use (4 − 1) =3 indicator variables, W₁, W₂, W₃. The observations are assumed to have the form

Y_i = b₀ + b₁X_i1 + b₂X_i2 +...+ b_p X_ip + a₁W_i1 + a₂W_i2+ a₃W_i3 + e_i,

i = 1, 2, ..., n (17.2)

where

(17.3)

Note that for each point i only one of W_i1, W_i2, W_i3 is equal to unity, the other two being zero.

Note also that an indicator variable is not needed for the final category as its effect is absorbed by the overall constant b₀.

18 Experimental Designs

The topic of experimental design concerns the important issue of selecting the values of the explanatory variables to be used in making each run of an overall simulation experiment. There are many useful designs, depending on aim of the simulation experiment. We shall only consider a few of the most useful designs. Useful brief introductions are given by Kleijnen (2007) and Sanchez (2008).

There is one useful point to note when considering designs. Equation (15.12) giving the variance-covariances of the estimates of the coefficients in terms of the design matrix X, is a very useful formula. Firstly it provides a simple test for checking that all the coefficients which are to be included in the model can actually be estimated using the proposed design. All that is required is to check if the matrix X^TX appearing in (15.12) is invertible, this condition being both necessary and sufficient to ensure that all the coefficients in the vector b can be estimated. If all the coefficients can be estimated, the diagonal entries in the inverted matrix, (X^TX)^-1, being simply the variances of the estimators of the coefficients multiplied by , can then be used to check how well individual coefficents can be estimated. This allows different competing designs to be easily compared.

18.1 Main Effects Model

18.1.1 Factorial Designs

Consider the main effects model (14.1). Here the value of any given b_j could be estimated by making two runs with X_j set to different values in the two runs, whilst the other factors are unchanged in the two runs. This is the so-called method of varying values one at a time. This method is not usually very efficient compared with what are called (full) factorial designs. The simplest of these is where it is assumed that each factor can take just one of two possible values. These are conventionally assumed to be standardized so as to be +1 and -1, representing ‘High’ and ‘Low’ settings. Designs are represented in the literature using such normalized settings. In a full factorial experiment all possible combinations of factors settings at these two levels are taken, yielding 2^p design points in all. Table 18.1 shows the 8 design points of a three factor experiment.

Table 18.1: Variable settings for 2³ factorial design

_____________________________________________

Variables

Design point X₁ X₂ X₃

_____________________________________________

1 -1 -1 -1

2 +1 -1 -1

3 -1 +1 -1

4 +1 +1 -1

5 -1 -1 +1

6 +1 -1 +1

7 -1 +1 +1

8 +1 +1 +1

_____________________________________________

We give two examples. The first involves just two factors.

Example 18.1. Figure 18.1 depicts the runs made in a one-at-a-time experiment involving two factors, and the corresponding full 2² factorial experiment. ANOVATwoMainEffects.xls compares the effectiveness of these two designs.

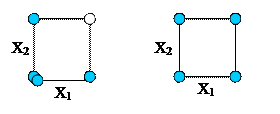
Figure 18.1 One at a time Experiment and Full Factorial Experiment for 2 Factors

(ANOVATwoMainEffects.xls) It will be seen that in the one-at-a-time experiment the estimate of b₀ has variance whilst the estimates of the other coefficients all have variance . In contrast, in the full factorial experiment the estimates of all the coefficients have a smaller variance, . Moreover the design is orthogonal so that the coefficient estimates are all independent. This is a very useful property for a design to have as it means that contribution of a particular explanatory variable does not depend on those of other explanatory variables. Full factorial designs are always orthogonal. y

A full factorial experiment, when each factor is considered at two levels, has 2^p design points. This is often provides far more design points than we need to estimate all the unknown coefficients, including . A neat solution is to use a fractional factorial experiment, where only a given proportion of the full factorial design is used. An introduction to factorial designs is given in Law (2007). A typical fractional factorial design based on a 2^p full factorial design contains 2^{p – m} design points, with m chosen to ensure that main effects can be estimated adequately using just the fractional factorial design with its reduced number of design points. (The notation 2^{p – m is} standard to indicate the number of factors and the fraction of the full design being used.)

Half fractions are particularly easy to generate. To create a 2^{p – 1} factorial design, first set up the p columns ( this includes the X₀ column) of a full factorial experiment for (p - 1) factors. Then add one last column, (corresponding to the final pth factor) by multiplying together all the entries for the first (p - 1) factors.

Example 18.2. Figure 18.2 shows the designs for a one-at-a-time experiment and a fractional factorial experiment using a half-fraction, when there are three factors each being considered at just two levels. Notice that the basic one-at-a-time experiment has (p + 1) design points. This enables the coefficients to be estimated but not the variance . We compare this with the fractional factorial 2^3-1, as shown in the Figure 18.2.

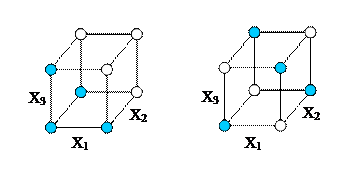
Figure 18.2 One at a time Experiment and 2^3-1 Fractional

Factorial Experiment for 3 Factors

ANOVAThreeMainEffects.xls compares the two experiments in this example. Note that as both designs has only 4 design points each, we cannot estimate as well as all the coefficients b, using either design. In the spreadsheet we simply replicate each design in its entirety to provide extra observations with which to estimate .

Exercise 18.1: Make this comparison using the spreadsheet. y

18.1.2 Plackett-Burman Designs

Even with the use of fractional factorial designs, it is often the case that a fractional factorial design cannot be found with a number of design points closely matched to the number of factors. Where a precise match is obtained the design is said to be saturated. Where main effects are concerned, Plackett-Burman (Plackett and Burman, 1946) designs are generalisations of fractional factorial designs which exist for n = 4, 8,…, There is no single comprehensive method for finding a design for n = 4t for all t, but the list is complete up to n = 100, and nearly so up to 200. Plackett-Burman designs are orthogonal.

19 Interactions

Fractional factorial and Plackett Burman designs enable main effects to be efficiently estimated assuming that interactions are negligible. However there may be uncertainty about this. A particularly serious concern is the problem of confounding. This is the situation where an interaction cannot be separated from a given main effect or from a given lower order interaction that is known to be important. Two such quantities which cannot be separately estimated in a given design are said to be confounded or aliased. Designs are usually classified according to the form of aliasing that they are subject to. A particular useful form of classification is the resolution of a design.

A design of resolution R (often denoted by Roman numerals) is one where an l-way interaction (with a main effect defined as a 1-way interaction) may possilby be confounded with an interaction of order R-l, but not one lower. Thus in a resolution III design, a main effect (i.e. where l = 1) may be confounded with an interaction of order 3-1 = 2 (i.e a two-way interaction) but not with another main effect. A resolution III design will therefore estimate main effects properly but only if it can be assumed that all two-way (and higher order) interactions are negligible. For a resolution IV design, a main effect may be confounded with an interaction of order R-1 = 4-1 = 3, but not with any two-way interactions. However a two-way interaction may be confounded with an interaction of order R-l = 4-2 = 2. Thus, the two-way interactions may be confounded with one another.

Exercise 19.1. What resolution is required to be able to estimate all the coefficients of a quadratic regression model?

20 Central Composite Designs

Designs with factors at only two levels cannot be used to assess all second order effects. 3^p factorial experiments can be used, but can lead to an unnecessary increase in the number of design points being added to an experiment.

A simple alternative is to use what are called central composite designs. Start with a 2^p or a Resolution 5 2^p-m fractional factorial, then add a centre point and two ‘star 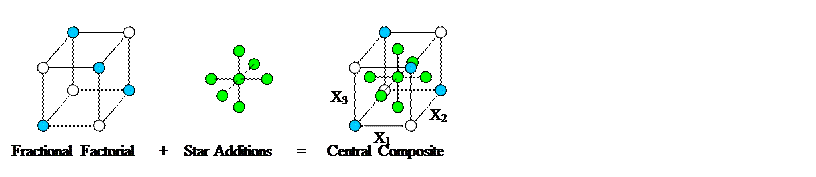Figure 20.1 Construction of a Central Composite Design

points’ for each factor. The centre point is simply X₀ = 1, X₁ = 0, X₂ = 0, … X_p = 0. The star points are X₀ = 1, X₁ = 0, X₂ = 0, …, X_i = -c, … , X_p = 0 and X₀ = 1, X₁ = 0, X₂ = 0, …, X_i = +c, … , X_p = 0, for i = 1, 2, …, p, where we can take c = 1, though other values are possible. Figure 20.1 depicts the case for three factors.

Example 20.1. ANOVAWSC04Optim.xls contains an example discussed in Cheng and Currie (2004) involving a simulation model of car performance depending on six factors. The objective was to find settings of the six factors to optimize the tuning of the car. The experiment therefore involves fitting a quadratic regression model to data obtained from simulation runs and then using the regression model to estimate the optimum (minimum) point.

21 Comments on Design of Experiments

The subject of design of experiments is a large one and we have only been able to touch on some of the main features. For further introductory material see Kleijnen (2007) and Sanchez (2008).

Though there is a large theory, the special circumstances of a particular practical application may still make it difficult to choose a good design. The spreadsheets provided in this course do however show how any given design can be rapidly assessed for how effective it is for estimating factors of interest, enabling designs to be set up and modified interactively.

22 Final Comments

This course has reviewed the process of constructing and fitting a statistical model to data whether this data arises from study of a real system or from a simulation.

The classical approach using the method of maximum likelihood has been described for fitting the model.

Two approaches for assessing the variability of fitted parameters have been discussed:

(i) The classical approach using asymptotic normality theory.

(ii) Bootstrap resampling.

Examples have been drawn mainly from regression and ANOVA applications. These have been for illustration only and I have not attempted to survey the range of statistical models likely to be encountered in practice, where typically different aspects of modelling need to be brought together. Krzanowski (1998) gives a very comprehensive but at the same time very accessible survey of the different types of situation commonly encountered. For instance, Krzanowski’s Example 6.1 gives data relating to factors affecting the risk of heart problems: social class, smoking, alcohol and so on. The data is ‘binary response’ data (i.e a patient reporting some form of ‘heart trouble’ or not). The factors are categorical (for example alcohol is coded as someone who drinks or someone who does not). The required model is therefore a logisitc regression model but with a linear predictor involving the categorical factors. Though this example has not been discussed explicitly in this course, all the elements needed to analyse it using either classical or bootstrap methods have been considered, and despite its apparent complexity, this model is quite capable of being tackled straightforwardly using the methods of this course.

In fact the spreadsheets given for the examples in this course use a number of VBA macros that enable various commonly occurring analyses to be carried out. These macros have been designed to be sufficiently flexible and accessible to be used in other applications and you are encouraged to make use of them in this way.

References

Banks, J. (1998). Handbook of Simulation. New York: Wiley.

Cheng, R.C.H. and Currie, C.S.M. (2004) Optimization by Simulation Metamodelling Methods. In Proceedings of the 2004 Winter Simulation Conference, eds R.G. Ingalls, M.D. Rossetti, J.S. Smith, and B.A. Peters. Piscataway: IEEE, 486-490

Chernick, M.R. (1999). Bootstrap Methods, A Practitioner's Guide. New York: Wiley.

D'Agostino, R.B. and Stephens, M.A. (1986). Goodness of Fit Techniques. New York: Marcel Dekker.

Davison, A.C. and Hinkley, D.V. (1997). Bootstrap Methods and their Application. Cambridge: Cambridge University Press.

Kleijnen, J.P.C. (2007). Regression Models and Experimental Designs: A Tutorial for Simulation Analysis. In Proceedings of the 2007 Winter Simulation Conference, eds S.G. Henderson, B. Biller, M.-H. Hsieh, J. Shortle, J.D. Tew and R.R. Barton. Piscataway: IEEE, 183-194.

Krzanowski, W.J. (1998). An Introduction to Statistical Modelling. London: Arnold.

Law, A.M. and Kelton, W.D. (1991). Simulation Modeling and Analysis, 2nd Ed., New York: McGraw-Hill.

Law, A.M. (2007). Simulation Modeling and Analysis, 4th Ed., New York: McGraw-Hill.

Plackett, R.L. and Burman, J.P. (1946). The Design of Optimum Multifactor Experiments, Biometrika, 33, 305-325.

Sanchez, S.M. (2008). Better than a Petaflop: The Power of Efficient Experimental Designs. In Proceedings of the 2008 Winter Simulation Conference, eds S.J. Mason, R.R. Hill, L. Mönch, O. Rose, T. Jefferson and J.W. Fowler. Piscataway: IEEE, 73-84.

Urban Hjorth, J.S. (1994). Computer Intensive Statistical Methods. London: Chapman & Hall.

Wetherill, G.B. (1981). Intermediate Statistical Methods. London: Chapman and Hall.