Critical Phenomena in Gravitational Collapse
In the early 90s Matthew Choptuik, then at the University of Texas in
Austin, made a detailed numerical study of the process of
gravitational collapse for one of the simplest forms of matter, called
a scalar field.
If the density of matter is weak and the effects of gravity are
therefore unimportant, the scalar field matter disperses to infinity,
like a ripple on a pond. But its own gravitational attraction will
tend to hold it together and slow down the dispersion. If the scalar
field matter is dense enough, a part of the matter never gets away to
infinity but reconverges and collapses to form a black hole. The
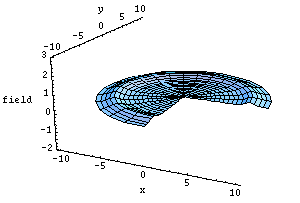
following schematic animations illustrate these two cases (dispersion
or black hole formation, respectively). Shown is a cross section
through a spherically symmetric situation (so that one space dimension
is suppressed). The scalar field amplitude is on the vertical
axis. The horizon of the black hole is represented by a cylinder.
In the low density case on the left, a spherically symmetric ripple of
scalar field matter runs into the center, through it, and out to
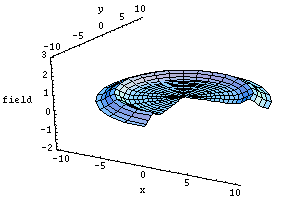
infinity. In the case on the right, the amplitude of the ripple is
larger and therefore the matter density is higher. A black hole forms
at the center when the density is highest, and only a part of the
matter escapes: the outgoing wave has a lower amplitude than the
ingoing wave. Click on the images to start the animation.
Choptuik studied precisely those cases where gravity nearly compensated
the escape tendency. He found very interesting and completely unexpected
phenomena:
- The scalar matter oscillates near the center of symmetry, always
showing the same structure but each time at smaller scales (and
each time on a shorter timescale). The center is reached after
infinitely many oscillations but in a finite time, without either
forming a black hole or escaping to infinity. Click on the picture
to see an animation of this echoing process. The matter density is
on the vertical axis, and radius is on the horizontal axis (so now
two out of three space dimensions are suppressed so that one can
see more detail.)
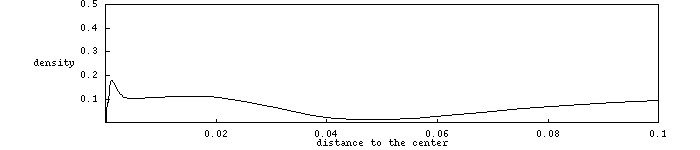 Note how the maximum of the density approaches the center and
oscillates faster and faster.
Note how the maximum of the density approaches the center and
oscillates faster and faster.
- This process generates an accumulation of oscillations at the
center of symmetry, creating a singularity with infinite curvature
there. But this singularity is not inside a black hole! It is
therefore called a naked singularity, something that it was
supposed not to be allowed by nature (the cosmic censor conjecture
of Roger Penrose). Because of Choptuik's results, Stephen Hawking
has conceded defeat in a famous bet he made with Kip Thorne and
John Preskill about the existence of naked singularities (New York
Times February 12, 1997 and February 16, 1997).
- Choptuik also found phenomena (power law behaviour, universality,
critical exponents...) which remind us of critical phase
transitions in statistical physics (for example a ferromagnet at
its Curie temperature or water at its triple point.) This is why
this research area of general relativity is now called "Critical
phenomena in gravitational collapse".
 |
 |
|




