Forecasting

4. Regression

The term regression refers to a certain type of statistical model that attempts to describe the relationship of one variable, called the dependent variable and usually denoted by Y, and a number of other variables X₁, X₂, ..., X_k , called the explanatory, or independent variables. We shall only consider the case of an additive error, e, where the relationship can be written as

Y = f(X₁, X₂, ..., X_k; b₀, b₁, ..., b_p) + e (4.1)

where f is a given function, known as the regression function. The function will depend on parameters or coefficients, denoted by b₀, b₁, ..., b_p. The parameter values are not known and have to be estimated. The number of regression parameters r = p+1 is not necessarily the same as k. Finally there is an additional uncertain element in the relationship, represented by the random variable e. The probability distribution of e is usually specified, but this specification is not usually complete. For example the distribution of e is often taken to be normal, N(0, σ^.2.), but with the variance, σ^.2, unknown.

Irrespective of the form of e, we assume that the expected value of e is

E(e) = 0

so that, assuming the explanatory variables are given, then the regression function is the expected value of Y

E(Y) = f(X₁, X₂, ..., X_k; b₀, b₁, ..., b_p) (4.2)

The simplest and most important relationship is linear regression.

Y = b₀ + b₁X₁ + b₂X₂ +...+ b_k X_k + e (4.3)

This is called simple linear regression if there is only one explanatory variable, so that k = 1, i.e.

Y = b₀ + b₁X₁ + e. (4.4)

When k > 1, the relationship is called multiple linear regression.

The above regression models are completely general and not specifically connected with forecasting. However forecasting is certainly an area of application of regression techniques. We will be examining three applications

(i) Use of polynomial regression for smoothing, with X = t (time).

(ii) Use of multiple linear regression for prediction.

(iii) Use of multiple linear regression for forecasting, with i = t (time).

Before considering these applications we summarize the main features of linear regression as a classical statistical technique. There is a huge literature on linear regression. A good description at a reasonably accessible level is Wetherill (1981). Draper and Smith (1966) is a good reference. A good Web reference is http://www.statsoftinc.com/textbook/stmulreg.html. For a derivation of the results see Draper and Smith for example.

4.1 Linear Regression

4.1.1 The linear regression model

The values of the coefficients in (4.3) , which for convenience we denote by a column vector

b = (b₀, b₁, ..., b_p)^T

(where the superscript T denotes the transpose), are usually unknown and have to be estimated from a set of n observed values {Y_i , X_i1, X_i2, , X_ik} i = 1, 2, ..., n. In linear regression, the relationship between the values of Y, and the X 's of each observation is assumed to be

Y_i = b₀ + b₁X_i1 + b₂X_i2 +...+ b_k X_ik + e_i, i = 1, 2, ..., n (4.5)

It is convenient to write this in the partial vector form

Y_i = X_ib+ e_i, i = 1, 2, ..., n

where X_i = (1, X_i1, X_i2, , X_ik) is a row vector. The full vector form is

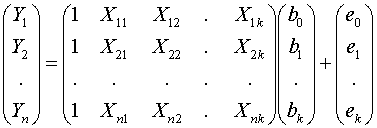(4.6)

ie

Y = Xb + e (4.7)

The values of the explanatory variables written in this matrix form is called the design matrix. In classical regression this is usually taken to be non random, and not to depend explicitly on time.

Exercise 4.1: Identify the observations Y and the design matrix X for the Bank Data example. Note that this example is typical of situations where regression is used in forecasting, in that the observations {Y_i, X_i1, X_i2, , X_ik} i = 1, 2, ..., t come from a time series. We have emphasised this here by using t as the subscript indicating the current time point rather than n.

[Web: Bank Data ]

4.1.2 Least Squares Estimation, and Sums of Squares

The most commonly used method of estimation is that of least squares (LS). This estimates b by minimizing the sum of squares

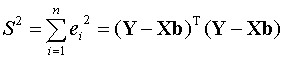
with respect to b. A more statistically satisfactory method is that of maximum likelihood. This latter method requires an explicit form to be assumed for the distribution of e, such as the normal, whereas least squares is distribution free. In the special case where the errors are assumed to be normally distributed then least squares and maximum likelihood methods are essentially equivalent.

The LS estimators are

= (X^TX)⁻¹X^TY

The estimate of the regression function at the ith observed value X_i = (1, X_i1, X_i2, , X_ik) is written as , and is calculated as

.

The total sum of squares (corrected for the overall mean) is

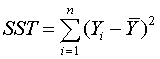
where 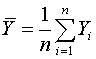. This decomposes into

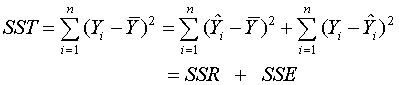
where

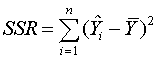
is called the regression sum of squares. This measures the reduction in total sum of squares due to fitting the terms involving the explanatory variables. The other term

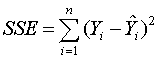
is called the (minimized) residual or error sum of squares and gives the variance of the total sum of squares not explained by the explanatory variables.

The sample correlation, , between the observations Y_i and the estimates can be calculated from the usual sample correlation formula and is called the multiple correlation coefficient. Its square turns out to be

.

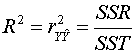This is called the coefficient of determination. R² is a measure of the proportion of the variance of the Y's accounted for by the explanatory variables.

The sums of squares each have an associated number of degrees of freedom and a corresponding mean square

(i) For SST: dfT = n − 1, and MST = SST/dfT

(ii) for SSR: dfR = k (# of coefficients − 1) and MSR = SSR/dfR

(iii) For SSE: dfE = n − k − 1 and MSE =SSE/dfE

Thus we have

dfT = dfR + dfE.

Under the assumption that the errors, e_i, are all independent and normally distributed, the distributional properties of all the quantities just discussed are well known.

If in fact the b_i i = 1,2,..., k are zero so that the explanatory variables are ineffective then the quantity

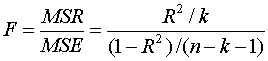
has the F-distribution with k and (n − k − 1) degrees of freedom. If the b_i are non zero the F tends to be larger.

These calculations are conventionally set out in the following analysis of variance (ANOVA) table

————————————————————————————

Source Sum of df MS F P

Squares

————————————————————————————

Regression SSR k SSR/k MSR/MSE P-value

Error SSE (n − k − 1) SSE/(n − k − 1)

————————————————————————————

Total SST (n − 1)

————————————————————————————

Exercise 4.2: Use the Worksheet array function LINEST to calculate the least squares estimates of the regression coefficients for the Bank Data. LINEST will provide SSR, SSE and F. Use the Worksheet function FDIST to calculate the P-value.

Produce the regression ANOVA table for the Bank Data. Use only the first 53 observations. The remaining observations will be used for model validation later. [Web: Bank Data ]

4.1.3 Individual Coefficients

Either the coefficient of determination, R ², or the F - ratio gives an overall measure of the significance of the explanatory variables. If overall significance is established then it is natural to try to identify which of the explanatory variable is having the most effect. Individual coefficients can be tested in the presence of all the other explanatory variables relatively easily.

Again we assume that the errors e_i are N(0, σ²) variables. Then the covariance matrix of is given by

Var() = (X^TX)⁻¹σ².

An estimate of σ ² is given by MSE:

.

If the true value of b_i = 0, so that the explanatory variable is not effective, then it is known that

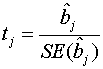
where is the standard error of has the t-distribution with (n − k − 1) degrees of freedom.

The P-value of t_j i.e. Pr(T > |t_j|) where T is a random variable having the t-distribution with (n − k − 1) degrees of freedom can then be found.

Alternatively, and rather better, is to calculate a 100(1 − α)% confidence interval for the unknown true value of b_j as

± t(α/2). .

Exercise 4.3: LINEST calculates and but not the P-values, Pr(T > |t_j|). For the Bank Data calculate these P-values and also the confidence intervals. Use the Worksheet functions TDIST and TINV. [Web: Bank Data ]

4.2 Multiple Linear Regression for Prediction

An application of the analysis of Section 4.1 above is to use of a set of explanatory variables X = (1, X₁, X₂, , X_k) to predict E(Y) from

.

Here time not explicitly involved. Thus we are not using the word predict in the sense of forecasting the future. We use 'predict' only in the sense that the fitted regression model is used to estimate the value of regression function that corresponds to a particular set of values of the explanatory variables.

4.2.1 Additional Explanatory Variables

In any regression model, including ones used with time series, one may consider introducing additional explanatory variables to explain more of the variability of Y. This is especially desirable when the error sum of squares, SSE is large compared with SSR after fitting the initial set of explanatory variables.

One useful type of additional variable to consider are what are called indicator variables. This often arises when one wishes to include an explanatory variable that is categorical in form. A categorical variable is one that takes only a small set of distinct values.

For example suppose we have a categorical variable, W, taking just one of four values Low, Medium, High, Very High. If the effect of W on Y is predictable then it might be quite appropriate to assign the values 1, 2, 3, 4 to the categories Low, Medium, High, Very High and then account for the effect of W using just one coefficient a:

Y_i = b₀ + b₁X_i1 + b₂X_i2 +...+ b_k X_ik + aW + e_i, i = 1, 2, ..., n

However if the effect of each of the different possible values of the categorical variable on Y is not known then we can adopt the following different approach. If there are c categories then we introduce (c − 1) indicator variables. In the example we therefore use (4 − 1) =3 indicator variables, W₁, W₂, W₃. The observations are assumed to have the form

Y_i = b₀ + b₁X_i1 + b₂X_i2 +...+ b_k X_ik + a₁W_i1 + a₂W_i2+ a₃W_i3 + e_i,

i = 1, 2, ..., n

where

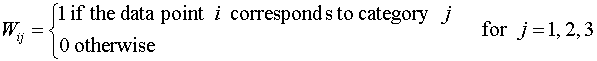
Note that for each point i only one of W_i1, W_i2, W_i3 is equal to unity, the other two being zero.

Note also that an indicator variable is not needed for the final category as its effect is absorbed by the overall constant b₀.

A typical application is to monthly data in which there is a seasonal component of uncertain effect. Thus month is the categorical variable. We need an indicator variable, D_i, for each of 11 months:

Note also that use of indicator variables to represent the effect of categorical variables can greatly increase the number of coefficients to be estimated.

Exercise 4.4: Introduce 11 monthly indicator variables for the Bank Data and fit the new regression model to the first 53 data points. [Web: Bank Data ]

4.2.2 Time Related Explanatory Variables

If the observations {Y_i, X_i1, X_i2, , X_ik} i = 1, 2, ..., t, come from time series then the explanatory variables are in this sense already time related. We may however include time itself as an explanatory variable, and even its powers. In the following model i, i², i³ are included as three additional variables.

Y_i = b₀ + b₁X_i1 + b₂X_i2 +...+ b_k X_ik + a₁W_i1 + a₂W_i2 + a₃W_i3 +

a₄i + a₅i² + a₆i³ + e_i, i = 1, 2, ..., t

Exercise 4.5: Introduce i as an explanatory variable well as the 11 monthly indicator variables for the Bank Data and fit the new regression model to the first 53 data points. [Web: Bank Data ]

4.2.3 Subset Selection

When the number of explanatory variables is large, then the question arises as to whether some of the explanatory variables might be omitted because they have little influence on Y. Many ways have been suggested for selecting variables.

(i) Best subset selection

(ii) Forward stepwise regression

(iii) Backward stepwise regression.

Makridakis et al. and Draper and Smith discuss this in more detail. Most packages offer routines for this. We do not discuss this further here. An important point is that when the design matrix is non-orthogonal, as invariably will be the case when the explanatory variable values arise from time series, then the rank order of significance of the coefficients as given by the P-values is not invariant, but depends on which coefficients happen to be included in the model.

Thus any statement about the significance of a coefficient, is always conditional on which other coefficients have been fitted. Nevertheless an initial assessment can be made simply by ordering the coefficients according to their P-value. The ones with large P-values can usually be omitted straight away.

Exercise 4.6: Assess which explanatory variables are important for the Bank Data, including in the assessment the time variable, i, as well as the 11 monthly indicator variables 53 data points. [Web: Bank Data ]

4.3 Local Polynomial Regression for Smoothing

The term linear refers to the way the unknown coefficients enter the regression equation, and not the explanatory variables. A good illustration of this is the polynomial regression equation

Y = b₀ + b₁X + b₂X ² +...+ b_k X ^k + e. (4.8)

If we set X₁ = X, X₂ = X ², ..., X_k = X ^k, then this shows that the polynomial model is just a special case of multiple linear regression. Thus polynomial regression can be analysed using the methods of multiple linear regression.

Smoothing, in order to identify the trend-cycle component, as discussed in Chapter 2, is a straightforward application of polynomial regression using equation (4.8) in the context of forecasting.

We use time, t, as the explanatory variable X. For each time point t we fit the regression model (4.8) to m = 2k + 1 points centred about t. For each time point t, the m data points used are assumed to be of the form

Y_i = b₀ + b₁i + b₂i ² +...+ b_p i ^p + e_i

i = t − k, t − k + 1, ... , t + k − 1, t + k.

The unknown b's are estimated in the usual way.

The degree of the polynomial, p, does not usually need to be very high; p = 1, 2, or 3 is adequate.

Exercise 4.7: Carry out local polynomial smoothing for Mutual Savings Bank data. Try p = 2, and m = 5. [Web: Mutual Savings Bank ].

4.3 Multiple Linear Regression for Forecasting

Suppose that the current time point is t, and that we have observations {Y_i, X_i1, X_i2, , X_ik} i = 1, 2, ..., t up to this point.

We now wish to forecast Y for time points i = t + 1, t + 2, ... , t + m. However rather than use one of the forecasts of Chapter 3, such as Holt's LES forecast on Y directly we feel that the estimate of E(Y_i) for i = t + 1, t + 2, ... , t + m, obtained from the multiple regression model of Y using X₁, X₂, , X_k as explanatory variables, will be a better forecast.

To be able to do this we need forecasts

G_i = (G_i1, G_i2, ... G_ik ) of X_i = (X_i1, X_i2, , X_ik)

for i = t + 1, t + 2, ... , t + m.

We can then use each of these forecasts in the predictor, , as the forecast of E(Y). i.e.

F_i = for i = t + 1, t + 2, ... , t + m

The forecasts G_i can be obtained in a number of ways, possibly exploiting relationships between the X₁, X₂, , X_k themselves. We shall not consider these possibilities in any detail. Instead we shall assume that the X_j behave independently of one another, and can therefore each be forecast separately using a method like Holt's LES.

We can however provide an estimate of the accuracy of these forecasts, using the standard error of the predictor . Given G_i, we have

for i = t + 1, t + 2, ... , t + m

where we can estimate σ using . Note that SE() does not give a true measure of the total variability of as it only expresses the variability of given the value of G_i, and does not take into account the variability in G_i itself.

Exercise 4.8: Produce forecasts for D(EOM) for the time periods i = 54, 55, ..., 59, for the Bank Data. [include as explanatory variables selected additional variables from the 11 monthly indicator variables] as follows:

1. Use Holt's LES method to forecast the values of the explanatory variables for i = 54, 55, ..., 59.

2. Then use the multiple regression model fitted in Exercise 4.5 to predict the corresponding Y_i.

3. Give confidence intervals for your forecasts of Y_i. [Web: Bank Data ]