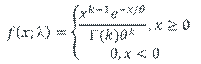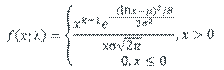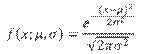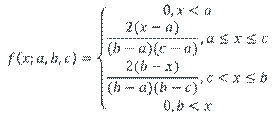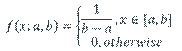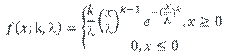Topic: Experimental Design and Analysis

 

Part II Input Modelling (NATCOR PartII 2015)

 

3.         Introduction

 

Input modelling for simulation models involves finding the best way of specifying inputs to the simulation model. These might be the distribution of service times in a queueing system; the arrival process into the simulated system; the process of modelling machine breakdowns in a manufacturing simulation; etc. A model is only as good as the data you use to build it or, as the saying goes, garbage in – garbage out. Consequently determining the correct input models and quantifying the uncertainty associated with the choice of input model is important.

 

In this section, we focus on situations in which data are available to fit input models and we use parametric distributions to describe the distribution of the data. Before describing the fitting process, we will discuss some useful ideas from mathematical statistics.

 

4.         Random Variables

 

The key concept of all statistics is the random variable. A formal definition of a random variable requires a mathematical foundation (and elaboration) that takes us away from the main focus of this course. We shall therefore not attempt a formal definition but instead adopt a simpler practical viewpoint. We therefore define a random variable simply as a quantity that one can observe many times but that takes different values each time it is observed in an unpredictable, random way. These values however will follow a probability distribution. The probability distribution is thus the defining property of a random variable. Thus, given a random variable, the immediate and only question one can, and should always ask is: What is its distribution?

 

We denote a random variable by an upper case letter X (Y, Z etc.). An observed value of such a random variable will be denoted by a lower case letter x (y, z etc).

 

In view of the above discussion, given a random variable, one should immediately think of the range of possible values that it can take and its probability distribution over this range.

 

The definition of most statistical probability distributions involves parameters. Such a probability distribution is completely fixed once the parameter values are known. Well known parametric probability distributions are the normal, exponential, gamma, binomial and Poisson. The next section provides a brief description of the best-known parametric probability distributions.

 

A probability distribution is usually either discrete or continuous. A discrete distribution takes a specific set of values, typically the integers 0, 1, 2,…. Each value i has a given probability pi of occurring. This set of probabilities is called its probability mass function.

 

Exercise 4.1: Plot the probability mass function of

(i)                  the binomial distribution, B(n, p)

(ii)                the Poisson distribution, P(λ)

Write down what you know of each distribution.                                                                                                                                               □

 

A continuous random variable, as its name implies, takes a continuous range of values for example all y ≥ 0. One way of defining its distribution is to give its probability density function (pdf), typically written as f(y). The pdf is not a probability, however it can be used to form a probability increment.  This is a good way to view the pdf.

 

Exercise 4.2: Write down the pdf of

            (i)         the normal distribution, . Normal Distribution

            (ii)        the gamma distribution, .  Gamma Distribution

 

Plot the density functions. Write down what you know about each distribution.               □

 

Exercise 4.3: Suppose that X is a continuous random variable with density f(x). Let Y be a function of X, say Y = h(X). What is the pdf, g(y) of Y, in terms of f(x)? Give the pdf of Y = X 2 when X is a standard normal random variable. What is the name of this random variable and what is the form of its pdf?                                                                                                                                                □

 

An alternative way of defining a probability distribution, which applies to either a discrete or continuous distribution, is to give its cumulative distribution function (cdf).

 

Exercise 4.4: Write down the main properties of a cdf.                                                                                                                         □

 

Exercise 4.5: Plot the cdf’s of each of the examples in the previous examples.                           □

 

Exercise 4.6: What is the relation between the pdf and the cdf for a continuous random variable? How is one obtained from the other?                                                                                                                     □

 

Exercise 4.7: Define the expected value of a random variable X in terms of its pdf f(x). Define the expected value of Y = h(X) in terms of the pdf of X.                                                                □

 

4.1. Empirical Distribution Functions

 

Consider first a single random sample of observations , for i  = 1, 2, ..., n. The empirical distribution function (EDF) is defined as:

 

.                                                             (4.1)

 

The EDF is illustrated in Figure 4.1. It is usually simplest to think of the observations as being ordered:

 

Y(1) < Y(2) < … < Y(n) .                                                               (4.2)

 

These are what are depicted in Figure 4.1. Note that the subscripts are placed in brackets to indicate that this is an ordered sample.

 

The key point is that the EDF estimates the (unknown) cumulative distribution function (CDF) of Y.

 

Fundamental Theorem of Sampling: As the size of a random sample tends to infinity then the EDF constructed from the sample will tend, with probability one, to the underlying cumulative distribution function (CDF) of the distribution from which the sample is drawn.

 

(This result when stated in full mathematical rigour, is known as the Glivenko-Cantelli Lemma, and it underpins all of statistical methodology. It guarantees that study of increasingly large samples is ultimately equivalent to studying the underlying population.)

 

Figure 4.1: EDF of the Yi ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

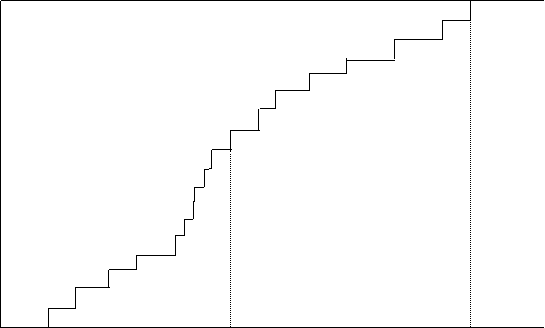
Y(1)
 

Y(j)
 

Y(n)
 
 

 

 

 


We can study the properties of the Yi  directly using the EDF, without bothering to fit a parametric model. If the Yi describe the input of a simulation model, this can be viewed of a way of ensuring that we do not generate values that could not exist in the real system. However, there are drawbacks such as the incomplete coverage of the range of feasible values and the inability to sample values outside of the range of observations.

 

The attraction of using the EDF directly, rather than a fitted parametric CDF, is that we make no assumption about the underlying distributional properties of Y. Thus Y can be either a continuous or a discrete random variable. Nor is it assumed to come from any particular family of distributions like the normal or Weibull. This flexibility is particularly important when the EDF is that of the output of a complex simulation, where it is possible that the distribution of the output may be unusual. For example it may well be skew, or possibly even multimodal.

 

5.         Fitting Parametric Distributions to Random Samples

 

Random samples are the simplest data sets that are encountered. A random sample is just a set of n independent and identically distributed observations (of a random variable). We write it as Y = {Y1, Y2, … Yn,} where each Yi represents one of the observations.

 

Parametric distributions are statistical distributions that we can write down mathematical expressions for that involve parameters. These parameters need to be estimated and this is the main focus of this and the next section. Before considering the fitting, it is worth reminding ourselves of the main characteristics of some of the most popular statistical distributions and these are given in Tables 5.1 (discrete distributions) and 5.2 (continuous distributions)

 

Table 5.1 Common Discrete Probability Distributions

 

Name

Description

Probability Mass Function

Poisson

Probability of a given number of events k occurring in a fixed interval of time or space.

Binomial

Probability of a number of successes k, in n independent yes/no experiments.

Geometric

Probability of the number of failures k, before the first success in a sequence of Bernoulli trials.

 

Table 5.2 Common Continuous Probability Distributions

 

Name

Description

Probability Density Function

Beta

Used to model the distribution of quantities that are bounded between 0 and 1 (although adding a constant or multiplying by a constant can change the range).

, xÎ(0,1)

Exponential

Useful for modelling the time between independent events, e.g. inter-arrival times. If inter-arrival times follow an exponential distribution, the number of arrivals in a given time follows a Poisson distribution.

Gamma

Used to model non-negative random variables (the exponential is a special case of the gamma distribution)

Lognormal

Often used to describe the distribution of a quantity that is the product of a number of different quantities.

Normal

Often used to describe the distribution of a quantity that is the sum of a number of different quantities, e.g. the sum of times required to complete an operation.

Triangular

Often used when no data are available but the minimum, maximum and most likely values are known.

Uniform

Used when there is an equal probability of the quantity taking on any value in a given range.

Weibull

Most often used to model the time to failure. The exponential is a special case of the Weibull.

 

A basic problem is when we wish to fit a parametric distribution to a random sample. This problem is an elementary form of modelling called input modelling.

 

Example 2.1 (continued): Suppose we are modelling a queueing system where service times are expected to have a gamma distribution and we have some actual data of the service times of a number of customers from which we wish to estimate the parameters of the distribution. This is an example of the input modelling problem. If we can estimate the parameters of the distribution, we will have identified the distribution completely and can then use it to study the characteristics of the system employing either queueing theory or simulation.                                                                                                                                           □

 

To fit a distribution, a method of estimating the parameters is needed. The best method by far is the method of maximum likelihood (ML). The resulting estimates of parameters, which as we shall see shortly possess a number of very desirable properties, are called maximum likelihood estimates (MLEs). ML estimation is a completely general method that applies not only to input modelling problems but to all parametric estimation problems. We describe the method next.

 

6.         Maximum Likelihood Estimation

 

Suppose Y = {Y1, Y2, …, Yn} is a set of observations where the ith observation, Yi, is a random variable drawn from the continuous distribution with pdf fi(y, θ) (i = 1, 2, …, n). The subscript i indicates that the distributions of the yi can all be different.

 

Example 6.1: Suppose Yi ~ N(μ, σ 2) all i. In this case

                                                                   (5.1)

so that the observations are identically distributed. The set of observations is therefore a random sample in this case.                                           □

 

Example 6.2: Suppose Yi ~ , i = 1, 2, ..., n. In this case one often writes

 

                                                                                         (5.2)

where

 

                                                                                         (5.3)

 

is called the regression function, and

 

                                    ~ N(0, σ 2)                                                                (5.4)

 

can be thought of as an error term, or a perturbation affecting proper observation of the regression function.                                                                                        □

 

In the example, the regression function is linear in both the parameters , and in the explanatory variable x. In general the regression function can be highly nonlinear in both the parameters and in the explanatory variables.

 

In Example 6.2, the pdf of Yi is

 

                                    .                     (5.5)

 

Thus Y is not a random sample in this case, because the observations are not all identically distributed. However ML estimation still works in this case.

 

We now describe the method. Suppose that y = {y1, y2, …, yn} is a sampled value of Y = {Y1, Y2, …, Yn}. Then we write down the joint distribution of Y evaluated at the sampled value y as:

 

                        .                                 (5.6)

 

This expression, treated as a function of θ, is called the called the likelihood (of the

 

 

 sampled value y). The logarithm:

 

        (5.7)

 

is called the loglikelihood.

 

The ML estimate, , is that value of which maximizes the loglikelihood.

 

The MLE is illustrated in Figure 6.1 in the one parameter case. In some cases the maximum can be obtained explicitly as the solution of the vector equation

 

                                                                                                    (15)

 

which identifies the stationary points of the likelihood. The maximum is often obtained at such a stationary point. This equation is called the likelihood equation. The MLE illustrated in Figure 6.1 corresponds to a stationary point.

 

In certain situations, and this includes some well-known standard ones, the likelihood equations can be solved to give the ML estimators explicitly. This is preferable when it can be done. However in general the likelihood equations are not very tractable. Then a much more practical approach is to obtain the maximum using a numerical search method.

 

Figure 6.1.   The Maximum Likelihood Estimator

 

 

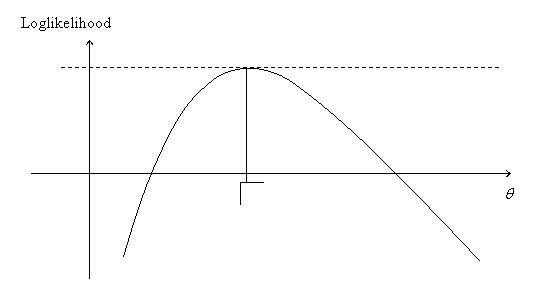
There are two immediate and important points to realise in using the ML method.

 

            (i) An expression for the likelihood needs to be written down using (6.6) or (6.7).

            (ii) A method has to be available for carrying out the optimization.

 

We illustrate (i) with some examples.

 

Exercise 6.1: Write down the likelihood and loglikelihood for

                                    (i) The sample of Example 6.1

                                    (ii) The sample of Example 6.2

                                    (iii) A sample of observations with the Bernoulli distributions (2.10).

                                    (iv) The sample of Example 2.3                                                

                                    Likelihood Examples                                                                 □

 

We now consider the second point, which concerns how to find the maximum of the likelihood. A number of powerful numerical optimizing methods exist but these can be laborious to set up. An exception is the readily accessible numerical optimizer Solver which can be called from an Excel spreadsheet. This can handle problems that are not too large. A more flexible alternative is to use a direct search method like the Nelder-Mead method. This is discussed in more detail in the following reference here:           Nelder Mead.

 

Exercise 6.2: NelderMeadDemo This is a VBA implementation of the Nelder-Mead Algorithm. Insert a function of your own to be optimized and see if it finds the optimum correctly.

 

Watchpoint: Check whether an optimizer minimizes or maximizes the objective. Nelder Mead usually does function minimization.                                                     □

 

Exercise 6.3: The following is a (random) sample of 47 observed times (in seconds) for vehicles to pay the toll at a booth when crossing the Severn River Bridge. Use the Nelder-Mead method to fit the gamma distribution G(α, β) to this data using the method of maximum likelihood. Gamma MLE

 

Watchpoints: Write down the loglikelihood for this example yourself, and check that you know how it is incorporated in the spreadsheet.                                                     □

 

 

7.         Accuracy of ML Estimators

 

A natural question to ask of an MLE is: How accurate is it? Now an MLE, being just a function of the sample, is a statistic, and so is a random variable. Thus the question is answered once we know its distribution.

 

An important property of the MLE, , is that its asymptotic probability distribution is known to be normal. In fact it is known that, as the sample size n → ∞,

 

                                     ~                                                        (7.1)

 

where is the unknown true parameter value and the variance has the form

 

                                    ,                                                       (7.2)

where

                                                                                      (7.3)

is called the information matrix. Thus the asymptotic variance of  is the inverse of the information matrix evaluated at . Its value cannot be computed precisely as it depends on the unknown , but it can be approximated by

 

                                    .                                                           (7.4)

 

The expectation in the definition of  is with respect to the joint distribution of Y and this expectation can be hard to evaluate. In practice the approximation

 

                                     '                                     (7.5)

 

where we replace the information matrix by its sample analogue, called the observed information, is quite adequate. Practical experience indicates that it tends to give a better indication of the actual variability of the MLE. Thus the working version of (7.1) is

 

                                     ~                                                         (7.6)

 

The second derivative of the loglikelihood, , that appears in the expression for  is called the Hessian (of L). It measures the rate of change of the derivative of the loglikelihood. This is essentially the curvature of the loglikelihood. Thus it will be seen that the variance is simply the inverse of the magnitude of this curvature at the stationary point.

 

Though easier to calculate than the expectation, the expression  can still be very messy to evaluate analytically. Again it is usually much easier to calculate this numerically using a finite-difference formula for the second derivatives. The expression is a matrix of course, and the variance-covariance matrix of the MLE is the negative of its inverse. A numerical procedure is needed for this inversion.

 

The way that (7.6) is typically used is to provide confidence intervals. For example a (1-α)100% confidence interval for the coefficient θ1 is

 

                                                                                             (7.7)

 

where is the upper 100α/2 percentage point of the standard normal distribution.

 

Often we are interested not in θ directly, but some arbitrary, but given function of θ, g(θ) say. ML estimation has the attractive general invariant property that the MLE of

g(θ) is

                                    .                                                                    (7.8)

 

An approximate (1-α)100% confidence interval for g(θ) is then

 

                                                    (7.9)

 

In this formula the first derivative of g(θ) is required. If this is not tractable to obtain analytically then, as with the evaluation of the information matrix, it should be obtained numerically using a finite-difference calculation.

 

Summarising it will be seen that we need to

            (i)                     Formulate a statistical model of the data to be examined. (The data may or may not have been already collected. The data might arise from observation of a real situation, but it might just as well have been obtained from a simulation.)

            (ii)        Write down an expression for the loglikelihood of the data, identifying the parameters to be estimated.

            (iii)       Use this in a (Nelder-Mead say) numerical optimization of the loglikelihood.

            (iv)       Use the optimal parameter values to obtain estimates for the quantities of interest.

            (v)                    Calculate confidence intervals for these quantities.

 

Example 7.1: Suppose that the gamma distribution  fitted to the toll booth data of Exercise 6.3 is used as the service distribution in the design of an M/G/1 queue. Suppose the interarrival time distribution is known to be exponential with pdf

 

                                                                                     (7.10)

 

but a range of possible values for the arrival rate, λ, needs to be considered.

 

Under these assumptions the steady state mean waiting time in the queue is known to be

                                    .                                        (7.11)

 

Plot a graph of the mean waiting time  for the queue for 0 < λ < 0.1 (per second), assuming that the service time distribution is gamma: . Add 95% confidence intervals to this graph to take into account the uncertainty concerning  because estimated values  have been used. Gamma MLE                             □

 

Example 7.2: Analyse the Moroccan Data of Example 2.3. Fit the model

 

                           i = 1,2, .... 32

 

where xi is the age group of the ith observation,

 

                        ,

and

                         ~ N(0, θ12).                         

Regression Fit Morocco Data                           □

 

 

The previous two examples contains all the key steps in the fitting of a statistical model to data. Both examples involve regression situations. However the method extends easily to other situations like the Bernoulli model of Equation (2.10).

 

 

Example 7.3: Analyse the Vaso Constriction Data by fitting the Bernoulli model of Equation (2.10) using ML estimation.                                                            □

 

 

8          Goodness of Fit Testing

 

8.1 Classical Goodness of Fit

 

We consider the natural question: Does the model that we have fitted actually fit the data very well? For instance in Exercise 6.3 we fitted a gamma distribution to toll booth service time data, but does the fitted gamma distribution capture the characteristics of the data properly?

 

The classical way to answer this question is to use a goodness of fit test (GOF test). A very popular test is the chi-squared goodness of fit test. The main reason for its popularity is that it is relatively easy to implement. The test statistic is easy to calculate and moreover it has a known chi-squared distribution, under the null, which makes critical values easy to obtain.

 

However the chi-squared test has two obvious weaknesses. It is actually not all that powerful, and it has a certain subjective element because the user has to divide the data into groups of her/his own choosing.

 

The best general GOF tests directly compare the EDF with the fitted CDF. Such tests are called EDF goodness of fit tests. In the past the Kolmogorov-Smirnov test has been the most popular, but the Cramér - von Mises test and the Anderson - Darling test, defined below, are generally more powerful and should be used in preference. The trouble with these tests is that, because of their sensitivity, their critical values are very dependent on the model being tested, and on whether the model has been fitted (with parameters having to be estimated in consequence). This means that different tables of test values are required for different models (see d’Agostino and Stephens, 1986).

 

First we describe EDF tests in more detail. Applying the Fundamental Theorem of Section 4, we see that a natural way to test if a sample has been drawn from the distribution with CDF F0(y), is to compare  with F0(y) by looking at some quantity involving the difference  – F0(y). Such an EDF test statistic typically has the form

 

                        .

 

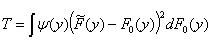Here y(y) is a weighting function. Special cases are the Cramér-von Mises test statistic:

                       

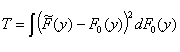
where y(y) = 1, and the Anderson-Darling test statistic:

 

                       

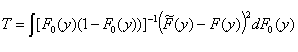
where y(y) = [F0(y)(1 – F0 (x))]-1 .

 

At first sight such GOF test statistic seem difficult to calculate involving a nasty integration. In fact things are much more straightforward than this. For example, the Anderson-Darling statistic (which is conventionally denoted by A2) is easily calculated using the equivalent formula

 

                       

 

where  is the value of the fitted CDF at the ith ordered observation.

 

The basic idea in using a goodness of fit test statistic is as follows. When the sample has really been drawn from F0(y) then the value of the test statistic will be small. This follows from the Fundamental Theorem of Section 4 which guarantees that  will be close in value to F0(y) across the range of possible y values. Thus T will be small. Nevertheless because the test statistic is a random quantity, it will have some variability according to a null distribution depending on the sample size n. If the null distribution is known then we can assess an observed value of T against this distribution. If the sample is drawn from a distribution different from F0(y) then the T will be large. Statistically, what is conventionally called its p - value will then be small, indicating that the distribution has not been drawn from the supposed null distribution.

 

Figure 8.1 illustrates the process involved in calculating a GOF test statistic for the parametric case. Two cases are shown. In both cases the distribution from which Y has been drawn is assumed to be , but where  is unknown; thus in each case  has been fitted to the random sample Y giving the ML estimate  of . However in the first case  is the correct model. Thus  will be the EDF of a sample drawn from  which will therefore converge to this distribution. In the second case the true model, , is different from , and may even involve a set of parameters  that is different from .  Thus the EDF  in this second case will not converge to , but to . Thus in the second case, T, which is a measure of the difference between the two, will be larger than in the first case.

 

The null situation is the first case where we are fitting the correct model. We need to calculate the distribution of T for this case. A complication arises because the difference between  and  is smaller than the difference between  and the unknown true. This is because the fitted distribution  will follow the sample more closely than  because it has been fitted to the sample. This has to be allowed for in calculating the null distribution of the test statistic.

 

 

Figure 8.1: Process Underlying the Calculation of a GOF Test, T

 

 

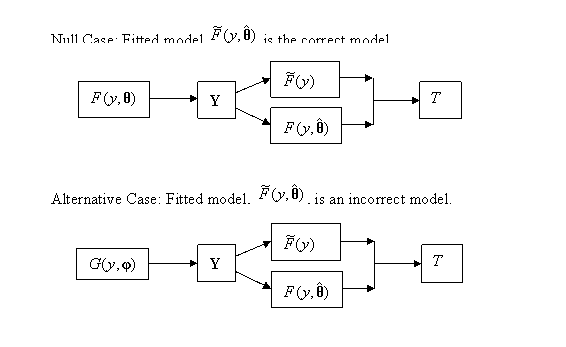
It will be seen that the GOF test hinges on being able to calculate the null distribution. This is a big issue and has meant that many potentially powerful test statistics, like the Cramér - von Mises, have not been fully utilized in practice because the null distribution is difficult to obtain.

 

In the next subsection we show how resampling provides a simple and accurate way of resolving this problem.

 

9          Bootstrapping a GOF statistic

 

If we could obtain many values of T using the null case calculation of the GOF statistic depicted in Figure 8.1, then the EDF of the Ti will converge to the CDF of T.  This is almost certainly too expensive or impractical to do. However we can get a close approximation by simply replacing the unknown  by its MLE . This is precisely the parametric bootstrap process. We provide some details of the parametric bootstrap in the next subsection but these will not be discussed in the lectures. More details can be found in Cheng and Currie (2009).

 

All being well  will be close in value to . Thus the distributional properties of the  will be close to those of a set of obtained under the null case calculation of Figure 8.1.

 

The parametric bootstrap method as it applies to a GOF statistic is illustrated in more detail in Figure 9.1, where  is the EDF of the bootstrap sample , and  is the bootstrap MLE of obtained from the bootstrap sample

 

Example 9.1: Examine whether the gamma model is a good fit to the toll booth data. Examine also whether the normal model is a good fit to the toll booth data. Use the Anderson-Darling goodness of fit statistic A2, previously given.

Gamma Fit Toll Booth Data                  Normal Fit Toll Booth Data                  □

 

 

 

Figure 9.1: Bootstrap Process to Calculation the Distribution of a GOF Test, T

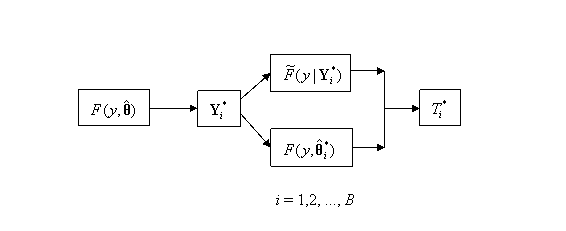
9.1 (Extension)           The Parametric Bootstrap

There are two versions of bootstrapping – the simple bootstrap and the parametric bootstrap. As the parametric bootstrap is of particular relevance to GOF tests, we only describe parametric bootstrapping here.

 

Suppose we have fitted a parametric model to data. If the parametric model is the correct one and describes the form of the data accurately, then the fitted parametric model will be a close representation of the unknown true parametric model. We can therefore generate bootstrap samples not by resampling from the original data, but by sampling from the fitted parametric model. This is called the parametric bootstrap. The basic process is depicted in Figure 9.2.

 

Figure 9.2: Parametric Bootstrap Process

 

 

 

                                                                                                                                    □
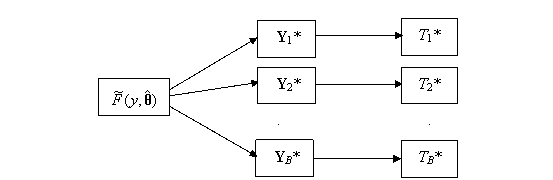