Let 
be the ground surface of the modeled region.
(We stress again that we are using a Cartesian coordinate system.)
The discussion in the last chapters and the model derivation in
Chapter 1 have shown that we are able to calculate
not only the pollutant concentration in certain compartments, which can
be anything from ecotrophic levels down to organs in individuals,
but that we can also calculate the effect of a pollutant on certain cell
populations in terms of toxicity and carcinogenicity. What remains
is to find an agglomeration of the different effects on the different
levels into one value. The minimization of all the quantified effects
simultaneously is evidently a multicriteria problem for which the knowledge
of some approximation of the efficient set would be of great use.
However, the high computational demands to compute such an approximation
as well as methodological difficulties force us at the present moment to
globalize all the different effects by way of a utility function.
The choice of such a utility is nontrivial, and it does not seem to be
clear what effect a corresponding choice has on the solutions of the resulting
single-criterion optimization problem. We prefer at the present moment to
globalize all the different effects by way of a weighting function. It is clear
that some of the efficient points of the abovementioned multicriteria problem
will be missed in this way [9]. However, scalarizations with,
e. g., the weighted max-norm, capable of computing all efficient
points [16], lead to nondifferentiable problems or problems with a
possibly large number of constraints, thereby adding computational costs
which might well be able to prohibite the computation of a solution.
Let 
be the number of compartments and 
be the pollutant
mass in compartment k (
) at the point 
and time
. Furthermore, let 
be the number of cell populations in
compartment k and 
be the number of cells of type i in
compartment k (
) at the point and time
. Set 
. The modeler has then to
specify n + N real-valued weights 
(, ) (one for each compartment and one
for each cell population). Let 
be the vector of decision variables. The vector 
represents
the location of the pollutant emitter, while 
is the width of the
"smokestack" and 
is it's height. With the weights given as above,
define the function
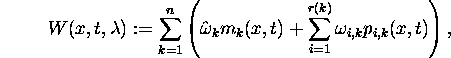
which measures the agglomerated effect of the decision 
at the
point at time .
Here, the dependance of 
and 
on has been skipped, as
it has been done above. The agglomeration of effects
over a time interval [0, T], T > 0, can be done in many ways. The method
employed in OLAF is the time integral over the effect
This approach has the advantage that
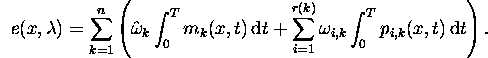
The time variable t is already discretized by the air
pollution model, and it is this equidistant discretization which is used in the
numerical evaluation of the integral above. Note that this approach allows
for hormetic values, i. e. 
for some points
and decisions 
. In such a case, the pollutant effect
has actually lead to a reaction of the individual's cell population residing
at x which can be interpreted as an increase in
health [2, 3].