As has been discussed elsewhere in these web pages, neutron stars, like most other objects in the universe, have a set of preferred oscillation frequencies at which they vibrate when perturbed in some way. Astrophysicists sub-divide these so-called `normal-modes of oscillation' into a handful of classes. The p-modes are the set of oscillations which consist mainly of pressure perturbations in the fluid; they can be thought of as sound waves trapped with the star. The g-modes are oscillations caused by the star's strong gravitational field trying to iron-out perturbations in the density profile. The r-modes exist only in rotating stars, and are caused by the Coriolis force generated by the rotation. The list of types of modes could go on and on.
What makes these normal modes interesting to relativists is that they cause the star to emit gravitational radiation. For instance, suppose an otherwise stationary star is perturbed so that a g-mode is excited. Then, if there are no energy losses inside the star (e.g. due to viscosity of the fluid), all of the energy of the g-mode oscillation is converted into gravitational wave energy. As time passes, the magnitude of the g-mode decreases, so that energy is conserved: the generation of gravitational wave energy occurs at the expense of kinetic energy of the fluid.
This wave emission is very exciting for gravitational wave astronomers, as it opens the possibility of learning about stars via gravitational wave observations. However, once the initial g-mode energy has been converted into gravitational wave energy, the star no longer emits gravitational waves. To use the technical language, the gravitational radiation reaction has damped the perturbation. When astrophysicists first thought about gravitational wave emission from stars, this was thought to be a general rule. However, Chandrasekhar in the 1960's found a counter-example, in which the gravitational radiation reaction seemed to amplify the oscillation of a rotating star. This is very important, as it greatly increases the strength of gravitational waves that might bathe the Earth. This counter-example was analysed by Friedman & Schutz, who in 1978 explained why this instability occurs in an elegant way. The instability of rotating stars has since become known as the `CFS-instability', after its discovers.
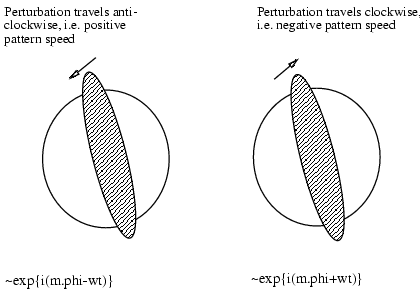
It is possible to understand the CFS instability via a simple, intuitive argument. Consider a non-rotating star, and a mode that at any given moment tends to elongate the fluid into some sort of bar shape, as shown symbolically by the shaded region on the left of the figure below. This deformation in shape travels with an angular velocity called the pattern speed, which we will define to be positive for the anti-clockwise motion indicated. The perturbation increases the angular momentum of the star as compared to its static, perturbation-free configuration; mathematically we can write delta J > 0. If excited, this mode emits gravitational radiation, which carries positive angular momentum. This positive angular momentum flux is subtracted from the positive angular momentum perturbation of the star; mathematically d(delta J)/dt <0. Clearly, this tends to decrease delta J and therefore tends to decrease the magnitude of the perturbation.
By symmetry, there must exist a mode that travels in the opposite sense, as
indicated on the right hand side of the figure, with a negative pattern
speed and a negative angular momentum perturbation; delta J < 0. This mode
emits negative angular momentum, which when subtracted from the negative
angular momentum of the mode gives d(delta J)/dt > 0, i.e. decreases its
magnitude. So far, there is no sign of instability.
| Schematic picture of the CFS instability. The circles denote the unperturbed neutron star surface, the shaded ellipses the (highly!) exaggerated surface shape when the star is perturbed. In the left-hand figure the perturbation travels in the anti-clockwise sense, in the right-hand figure it travels clockwise. |  |
However, let's consider what happens when the star itself is made to rotate. The key point that we must bear in mind is that the sign of the angular momentum carried by the gravitational waves depends only on the motion (i.e. whether it's clockwise or anti-clockwise) of the perturbation with respect to the laboratory frame, and has nothing to do with the motion of the mode with respect to the rotating star. On the other hand, the sign of the angular momentum perturbation of the star, delta J, depends only upon the motion of the mode relative to the star. These two points prove to be crucial.
For definiteness, let's assume that the stellar rotation is in the positive, anti-clockwise sense. Imagine starting off with a slowly rotating star, and gradually increasing the rotation rate. For the positive pattern speed mode, the perturbation of the angular momentum will remain roughly equal to its positive non-rotating value, delta J. As the star spins faster and faster, the mode will appear to rotate more rapidly as viewed from the laboratory frame, and therefore emits positive gravitational wave angular momentum more rapidly. It follows that, as the star's rotation rate is increased, this mode is damped more and more rapidly. Nothing interesting so far.
However, the situation is very different for the negative pattern speed mode. The perturbation of the angular momentum will remain roughly equal to its negative non-rotating value, delta J. However, the mode appears to move more slowly as viewed from the laboratory frame, decreasing the rate of angular momentum emission. When the star rotates sufficiently rapidly, the mode will appear to be `frozen' as viewed from the laboratory frame, the forward rotation of the star exactly compensating for the backward motion of the mode relative to the star. At this spin rate no gravitational waves are emitted, and no angular momentum is radiated. If the star spins even faster than this, the mode then starts to move anticlockwise as viewed from the laboratory frame, emitting positive angular momentum. This positive angular momentum must be subtracted from the negative angular momentum perturbation delta J, increasing the magnitude of delta J and therefore increasing the magnitude of the oscillation. The larger the perturbation grows, the more rapidly is radiated angular momentum, and the faster the mode grows---this is the promised instability! Using technical language, a sufficiently rapidly rotating star is unstable to gravitational radiation reaction.
In real neutron stars the situation is a little more complicated---internal energy losses such as viscous heating tend to suppress the CFS instability. This means that only extremely rapidly rotating stars (i.e. stars rotating close to their break-up velocity), for which the radiation reaction forces are very strong indeed, are likely to suffer this instability. However, recently Andersson and Kokkotas showed that the r-modes mentioned above might be a rather promising as gravitational wave sources, possibly going CFS-unstable at relatively modest rotation rates (possibly at less than one half of the break-up speed).