Hawking 1966

The results of Oppenheimer and Snyder were not taken seriously by many physicists because they not only predicted the existence of black holes, but also the existence of a singularity where the pressure becomes infinite. Thus any physical object that falls into the hole is not only trapped, but also eventually reaches a singularity where it is crushed to zero volume. It was felt that such predictions must be an artefact of the assumed spherical symmetry and would not persist in a more physically realistic situation.
In 1965 Roger Penrose used methods of global analysis to show that singularities are general phenomena which occur in gravitational collapse irrespective of symmetry. These ideas were then used by Stephen Hawking to establish the existence of cosmological singularities such as the big bang and work by Penrose, Hawking and Robert Geroch established a number of singularity theorems which showed that gravitational singularities occurred in very many situations.
| The singularity theorems seem to imply that either
the general theory of relativity breaks down or that there could be particles
whose histories did not exist before a certain time. My own opinion is that
the theory probably breaks down but only when quantum gravitational effects
become important.
Hawking 1966 |
 |
Intuitively a singularity is a place where the curvature of spacetime becomes infinite. However unlike other physical theories the notion of singularity in General Relativity is rather subtle. For electromagnetism for example one can talk about points in spacetime where the electric field diverges. It is not so easy to talk about points in spacetime where the curvature diverges, because in General Relativity spacetime itself is given by solutions of Einstein's equations, which by definition are not defined where the curvature is infinite. Instead singularities are characterised by points which are missing from the spacetime. These missing points can be detected by finding paths of particles or photons which terminate (and cannot be extended) because they run into the singularity. Thus a singular spacetime is one which is geodesically incomplete .
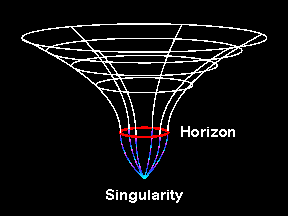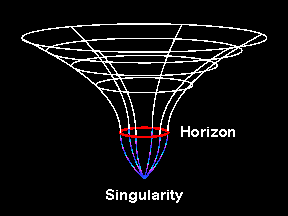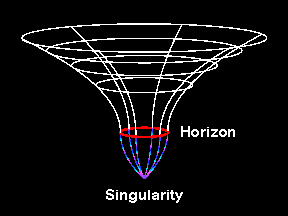 |
A key ingredient of the singularity theorems is that of a closed trapped surface . This is a surface where the gravitational field is so strong that outgoing photons are dragged inwards. |
The singularity theorems showed that a generic solution of Einstein's equations which satisfies certain reasonable physical conditions and contains a closed trapped surface is singular in the sense that it is geodesically incomplete. Thus although the theorems show that gravitational singularities are a general feature of gravitational collapse they do not say very much about the nature of the singularity. Although it is likely that the endpoint of a realistic collapse is a situation similar to the Schwarzschild singularity, in which there is a region where the gravitational forces become unbounded and crush matter to infinite density, other sorts of weaker singularity are possible. The analysis of these `weak singularities' is an area of mathematical research by the Southampton Relativity group.
The existence of a singularity however does not establish the existence of a black hole. A black hole is characterised by the existence region of spacetime with the property that nothing that enters the region can leave it (even photons). The boundary of this region is the event horizon which acts as a one way membrane between the black hole and the exterior. Thus although we know that singularities are a general feature of gravitational collapse we do not know if black holes are. It is possible that the singularity is not hidden by an event horizon but is naked . Although there exists no proof of the fact, there is considerable circumstantial support for the idea that nature prevents the occurrence of naked singularities in physically realistic gravitational collapse. This is known as the cosmic censorship hypothesis and was first suggested by Roger Penrose in 1969.
| We are thus presented with what is perhaps the most
fundamental unanswered question of general relativistic collapse theory,
namely: does there exist a `cosmic censor' who forbids the appearance of
naked singularities, clothing each one in an absolute event horizon.
Penrose 1969 |
 |
Unfortunately it is hard to give this idea a precise mathematical formulation without also being able to find counterexamples. Researchers at Southampton are trying to attack this problem by giving a new definition of singularities directly in terms of Einstein's equations. This approach called generalised hyperbolicity rules out some of the known counterexamples to the Cosmic Censorship conjecture.