A theory of curved space-time
Having formulated his Special theory, Einstein wanted to generalize it to
incorporate the gravitational interaction. It took him ten years to complete
this task. The final version of the theory was published in 1916. It is a relativistic
theory of gravitation (i.e. one consistent with Special Relativity), known as
General Relativity .
The key principle on which General Relativity is built derives from Galileo's
experiments in which he dropped bodies of different composition from the leaning
tower of Pisa. These experiments showed that all bodies fall with the same acceleration
irrespective of their mass and composition. This is known as the principle
of equivalence .
 |
This equivalence principle is best understood
in the context of Einstein's lift thought experiments where, neglecting
non-local effects, a body in a linearly accelerated rocket ship behaves
the same as one on the earth (experiencing the pull of gravitation).
On the other hand, a body in an unaccelerated rocket ship behaves the
same as one in free fall.
|
In the absence of gravitation we get back to Special Relativity
and a flat metric and so, in order to incorporate gravitation into the theory,
Einstein proposed that the metric should become curved. This means that the
geodesics become curved as well, which results in free bodies no longer moving
in straight lines when affected by gravity. The reason that a satellite
(like the Earth) orbits a central body (like the Sun) in Newtonian theory is
a combination of two effects: uniform motion in a straight line (Newton's first
law) and gravitational attraction between the two bodies (i.e. the satellite
"falls" under the attraction of the central body). In General Relativity, the
reason that a satellite orbits a central body is that the central body "curves
up" space (and, in fact, time as well) in its vicinity, and the satellite travels
on the "straightest path" which is available to it, namely on a curved
geodesic. One major difference between the two theories is that whereas Newtonian
theory describes how things move, and it does so remarkably accurately for ordinary
bodies, it does not really explain what is the cause. Einstein's theory neatly
provides answers for both these questions.
The General theory of Relativity can be stated
mathematically as
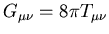
These are the so-called Einstein field equations. They correspond to 10 coupled
highly nonlinear partial differential equations. Their solution gives rise
to a curved spacetime metric from which one can obtain the geodesics and hence
investigate such things as the motion of free particles and light rays.
 |
The meaning of the Einstein equations can be summed up in the famous
words of John Archibald Wheeler:
"space tells bodies how to move and bodies tell space
how to curve"
|
General Relativity is concerned with studying the nature of these equations
and their solutions. Since few of the known exact solutions to Einstein's equations
describe physically relevant situations these studies are based on approximations,
such as post-Newtonian expansions or perturbation techniques, or numerical
simulations.
| One way to think of General Relativity is to use the
idea of a "rubber sheet geometry" where in the absence of gravitation the
sheet is flat, but a central massive body curves up the sheet in its vicinity
so that a free body (which would otherwise have moved in a straight line)
is forced to orbit the central body |
 |